Question

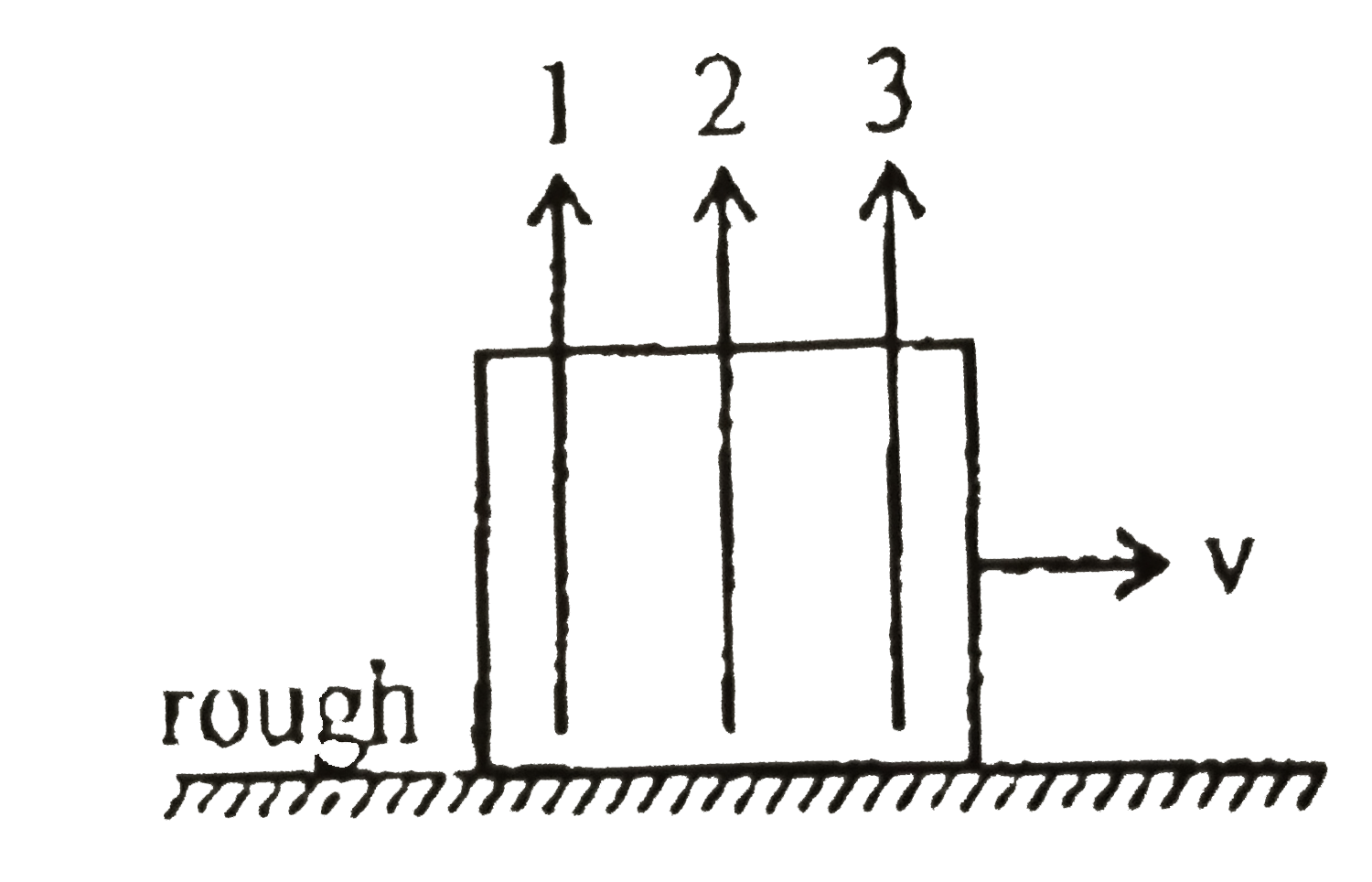
A horizontal force $F=\frac{mg}{3}$ is applied on the upper surface of a uniform cube of mass $m$ and slide a which is resting on a rough horizontal surface having $\mu =\frac{1}{2}$. The distance between lines of action of $mg$ and normal reation is

Options

A. `(a)/(2)`
B. `(a)/(3)`
C. `(a)/(4)`
D. None of these

Answer

B

Explanation

To solve the problem step by step, we need to analyze the forces acting on the cube and the moments about a point.

1. Identify the Forces Acting on the Cube:
- The weight of the cube, \( mg \), acts downward at the center of the cube.
- The normal force \( N \) acts upward at the base of the cube.
- A horizontal force \( F = \frac{mg}{3} \) is applied at the top of the cube.
- There is a frictional force \( f \) opposing the applied force, which will also be equal to \( F \) since the cube is at rest (static equilibrium).

2. Equilibrium Conditions:
- Since the cube is at rest, the net force in both horizontal and vertical directions must be zero.
- In the vertical direction:
\( N = mg \)
- In the horizontal direction:
\( f = F = \frac{mg}{3} \)

3. Determine the Moments about the Center of the Cube:
- Let's denote the center of the cube as point \( C \).
- The distance from the center \( C \) to the line of action of the weight \( mg \) is \( 0 \) (since it acts at the center).
- The distance from the center \( C \) to the line of action of the normal force \( N \) is \( x \) (which we need to find).
- The distance from the center \( C \) to the line of action of the applied force \( F \) is \( \frac{A}{2} \) (where \( A \) is the side length of the cube).

4. Setting Up the Moment Equation:
- The moments about point \( C \) must sum to zero:
\( \text{Clockwise moments} = \text{Counterclockwise moments} \)
- The friction force \( f \) creates a clockwise moment:
\( f \cdot \frac{A}{2} = \frac{mg}{3} \cdot \frac{A}{2} \)
- The normal force \( N \) creates a counterclockwise moment:
\( N \cdot x = mg \cdot x \)

5. Equating the Moments:
- The equation becomes:
\( \frac{mg}{3} \cdot \frac{A}{2} = mg \cdot x \)
- Simplifying this, we can cancel \( mg \) from both sides (since \( mg \neq 0 \)):
\( \frac{1}{3} \cdot \frac{A}{2} = x \)
- Thus, we find:
\( x = \frac{A}{6} \)

6. Finding the Distance Between Lines of Action:
- The distance between the lines of action of \( mg \) and \( N \) is \( x \).
- Therefore, the distance is:
\( x = \frac{A}{3} \)

Final Answer:
The distance between the lines of action of \( mg \) and the normal reaction \( N \) is \( \frac{A}{3} \).