A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
(a) 8:1
(b) 9:7
(c) 4:3
(d) 5:3
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the two masses connected by a string over a pulley and use Newton's second law of motion.
1. Identify the Forces:
- For mass m1 (which is moving downwards), the forces acting on it are:
- Weight: m1g (downwards)
- Tension: T (upwards)
- For mass m2 (which is moving upwards), the forces acting on it are:
- Weight: m2g (downwards)
- Tension: T (upwards)
2. Write the Equations of Motion:
- For mass m1:
m1g−T=m1a(1)
- For mass m2:
T−m2g=m2a(2)
3. Substitute the Given Acceleration:
- We know that the acceleration a=g8. Substitute this into equations (1) and (2):
- For equation (1):
m1g−T=m1(g8)
Rearranging gives:
T=m1g−m1(g8)=m1g(1−18)=m1g(78)(3)
- For equation (2):
T−m2g=m2(g8)
Rearranging gives:
T=m2g+m2(g8)=m2g(1+18)=m2g(98)(4)
4. Set Equations (3) and (4) Equal:
- Since both expressions equal T, we can set them equal to each other:
m1g(78)=m2g(98)
5. Cancel g from Both Sides:
- g cancels out from both sides:
m1(78)=m2(98)
6. Rearranging the Equation:
- Rearranging gives:
m1m2=97
7. Conclusion:
- The ratio of the masses m1 to m2 is:
m1m2=97
Final Answer:
The ratio of the masses m1 and m2 is 9:7.
---
- For mass m1 (which is moving downwards), the forces acting on it are:
- Weight: m1g (downwards)
- Tension: T (upwards)
- For mass m2 (which is moving upwards), the forces acting on it are:
- Weight: m2g (downwards)
- Tension: T (upwards)
- For mass m1:
m1g−T=m1a(1)
- For mass m2:
T−m2g=m2a(2)
- We know that the acceleration a=g8. Substitute this into equations (1) and (2):
- For equation (1):
m1g−T=m1(g8)
Rearranging gives:
T=m1g−m1(g8)=m1g(1−18)=m1g(78)(3)
- For equation (2):
T−m2g=m2(g8)
Rearranging gives:
T=m2g+m2(g8)=m2g(1+18)=m2g(98)(4)
- Since both expressions equal T, we can set them equal to each other:
m1g(78)=m2g(98)
- g cancels out from both sides:
m1(78)=m2(98)
- Rearranging gives:
m1m2=97
- The ratio of the masses m1 to m2 is:
m1m2=97
The ratio of the masses m1 and m2 is 9:7.
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
Similar Questions
A light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically).If the acceleration of the system is g/8 then the ratio of masses "m_(1)" to "m_(2)" is "(" take "m_(1)>m_(2)]
View SolutionString going over a pulley connects two blocks of masses m, and my. String and pulley are light. Calculate acceleration of centre of mass of blocks system.

View Solution
Knowledge Check
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of masses is
A8:1B4:3C5:3D9:7A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A8:1B9:7C4:3D5:3Two bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
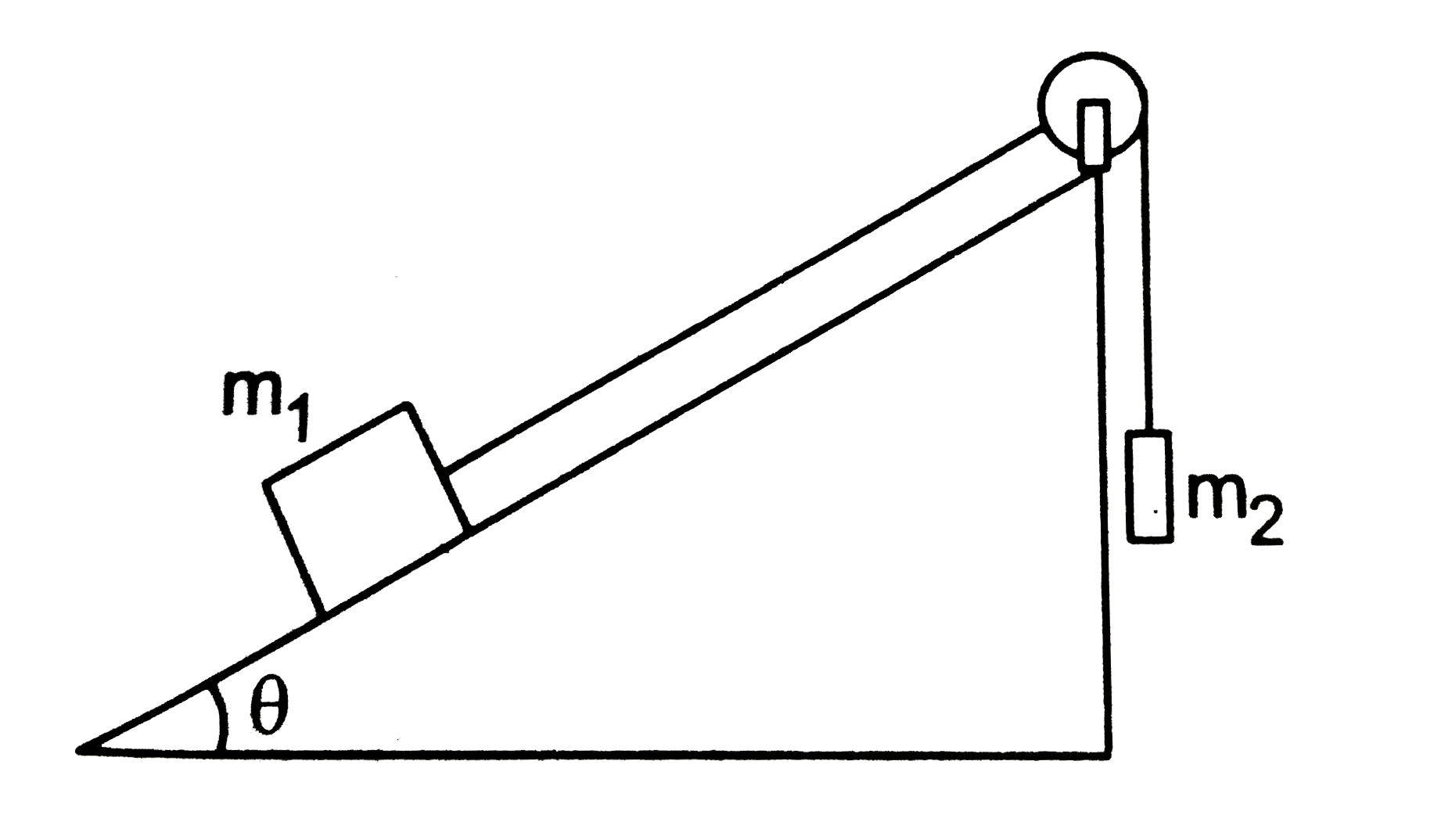 Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθ
Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθ
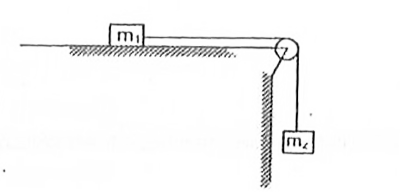
A block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionTwo bodies of masses 2kg and 3kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string (g=10ms−2)
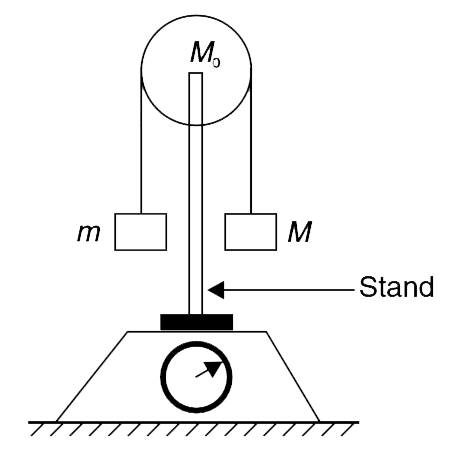
View SolutionA pulley is mounted on a stand which is placed over a weighing scale. The combined mass of the stand and the pulley is M0. A light string passes over the smooth pulley and two masses m and M (gt m) are connected to its ends (see figure). Find the reading of the scale when the two masses are left free to move.
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo bodies of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View Solution
