A long straight vertical conductor carries a current of 8A in the upward direction. What the magnitude of the resultant magnetic induction at a point in the horizonatal plane at a distance of 4 cm from the conductor towards South? (The horizontal compo-nent of earth's magnetic induction =4×10−5T)
2√2×10−5T
4√2×10−5T
4×10−5T
2×10−5T
The correct Answer is:B
To solve the problem of finding the resultant magnetic induction at a point in the horizontal plane at a distance of 4 cm from a long straight vertical conductor carrying a current of 8 A, we can follow these steps:
1. Identify the Given Values:
- Current (I) = 8 A (upward direction)
- Distance from the conductor (d) = 4 cm = 0.04 m (convert to meters)
- Horizontal component of Earth's magnetic induction (B2) = 4 × 10^(-5) T (towards the south)
2. Determine the Magnetic Field (B1) due to the Conductor:
The magnetic field (B1) at a distance d from a long straight conductor carrying current I is given by the formula:
B1=μ0I2πd
where μ0 (permeability of free space) = 4π×10−7T m/A.
3. Substitute the Values into the Formula:
B1=(4π×10−7)×82π×0.04
Simplifying this:
B1=(4×8)×10−72×0.04
B1=32×10−70.08
B1=4×10−5T
4. Calculate the Resultant Magnetic Induction (B_net):
The resultant magnetic induction (B_net) at the point is the vector sum of B1 and B2. Since B1 is directed towards the west (due to the right-hand rule) and B2 is directed towards the south, we can use the Pythagorean theorem:
Bnet=√B21+B22
Substituting the values:
Bnet=√(4×10−5)2+(4×10−5)2
Bnet=√2×(4×10−5)2
Bnet=4√2×10−5T
5. Final Result:
The magnitude of the resultant magnetic induction at the specified point is:
Bnet=4√2×10−5T
- Current (I) = 8 A (upward direction)
- Distance from the conductor (d) = 4 cm = 0.04 m (convert to meters)
- Horizontal component of Earth's magnetic induction (B2) = 4 × 10^(-5) T (towards the south)
The magnetic field (B1) at a distance d from a long straight conductor carrying current I is given by the formula:
B1=μ0I2πd
where μ0 (permeability of free space) = 4π×10−7T m/A.
B1=(4π×10−7)×82π×0.04
Simplifying this:
B1=(4×8)×10−72×0.04
B1=32×10−70.08
B1=4×10−5T
The resultant magnetic induction (B_net) at the point is the vector sum of B1 and B2. Since B1 is directed towards the west (due to the right-hand rule) and B2 is directed towards the south, we can use the Pythagorean theorem:
Bnet=√B21+B22
Substituting the values:
Bnet=√(4×10−5)2+(4×10−5)2
Bnet=√2×(4×10−5)2
Bnet=4√2×10−5T
The magnitude of the resultant magnetic induction at the specified point is:
Bnet=4√2×10−5T
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
A long straight vertical conductor carries a current of 8A in the upward direction. What the magnitude of the resultant magnetic induction at a point in the horizonatal plane at a distance of 4 cm from the conductor towards South? (The horizontal compo-nent of earth's magnetic induction =4×10−5T)
View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionA long straight wire in the horizontal plane carries a current of 50A in north to south direction. Give the magnitude and direction of →B at a point 2⋅5m east of the wire.
View SolutionTwo long parallel conductors cany currents i1=3A and i2=3A both are directed into the plane of paper. The magnitude of resultant magnetic field at point 'P, is
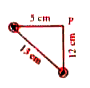 View Solution
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View SolutionA long straight current carrying conductor has a current from -z to +z, then find the magnetic induction at a point P(x, y, 0) in vectorial notation (ˆi,ˆj,ˆk) are unit vector along x,y, z axis)
 View Solution
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionA straight conductor of length 32 cm carries a current of 30A. Magnetic induction at a point which is in air at a perpendicular distance of 12cm from the mid point of the conductor is
View Solution

