A man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed 2 m/s . He is running on the cart , so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart . What is the speed of the centre of the mass of the system ?
1.5 m/s
1 m/s
3 m/s
Zero
To find the speed of the center of mass of the system consisting of a man and a cart, we can follow these steps:
Step 1: Identify the masses and velocities
- Mass of the man, m1=80kg
- Mass of the cart, m2=40kg
- Velocity of the cart, v2=2m/s (in the positive direction)
- Velocity of the man relative to the cart, v1,relative=−3m/s (opposite to the motion of the cart)
Step 2: Calculate the velocity of the man with respect to the ground
To find the velocity of the man with respect to the ground, we add the velocity of the cart to the relative velocity of the man:
v1=v1,relative+v2=−3m/s+2m/s=−1m/s
This means the man is moving at −1m/s with respect to the ground.
Step 3: Calculate the velocity of the center of mass
The velocity of the center of mass (vcm) of the system can be calculated using the formula:
vcm=m1v1+m2v2m1+m2
Substituting the values we have:
vcm=(80kg)(−1m/s)+(40kg)(2m/s)80kg+40kg
vcm=−80+80120=0120=0m/s
Conclusion
The speed of the center of mass of the system is 0m/s.
---
- Mass of the man, m1=80kg
- Mass of the cart, m2=40kg
- Velocity of the cart, v2=2m/s (in the positive direction)
- Velocity of the man relative to the cart, v1,relative=−3m/s (opposite to the motion of the cart)
To find the velocity of the man with respect to the ground, we add the velocity of the cart to the relative velocity of the man:
v1=v1,relative+v2=−3m/s+2m/s=−1m/s
This means the man is moving at −1m/s with respect to the ground.
The velocity of the center of mass (vcm) of the system can be calculated using the formula:
vcm=m1v1+m2v2m1+m2
Substituting the values we have:
vcm=(80kg)(−1m/s)+(40kg)(2m/s)80kg+40kg
vcm=−80+80120=0120=0m/s
The speed of the center of mass of the system is 0m/s.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A horse has to pull a cart harder in the initial stange of his motion . Why ?
View SolutionA man of 80 kg attempts to jump from the small boat of mass 40 kg on to the shore. He can generate a relative velocity of 6 m/s between him and boat. His velocity towards shore is
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionA force F=2t2 is applied to the cart of mass 10 Kg, initially at rest. The speed of the cart at t = 5 s is -
View SolutionA cart is moving with a velocity 20m/s. Sand is being dropped into the cart at the rate of 50 kg/min. The force required to move the cart with constant velocity will be :-
View SolutionA man is standing on a cart of mass double the mass of man. Initially cart is at rest. Now, man jumps horiozontally with velocity u relative to cart. Then work done by man during the process of jumping will be

View SolutionA cart A of mass 50 kg moving at a speed of 20 km/h hits a lighter cart B of mass 20 kg moving towards it at a speed of 10 km/h. The two carts cling to each other. Find the speed of the combined mass after the collision.
View SolutionA man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. by what velocity the gun rebounds backwards
View SolutionAn 80kg man is riding on a 40kg cart travelling at a speed of 2.5m/s on a frictionless horizontal plane jumps off the cart, such that, his velocity just after is zero with respect to ground. The work done by him on th esystem during his jump is given as A4KJ (Ain integer). Find the value of A.
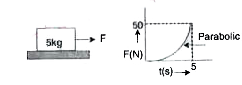
View SolutionA force F is applied to the initially stationary cart. The variation of force with time is shown in the figure. The speed of cart at t = 5 sec is
View Solution
