
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
2π√mk
π√mk+π√mk2
π√m3k2
π√mk+π√m2k
The correct Answer is:D
When the spring undergoes displacement in the downward direction it completes one-half oscillation while it completes another half oscillation in the upward direction. The total time period is
T=π√mk+π√m2k
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
A mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
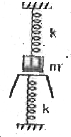 A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2kA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
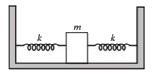 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
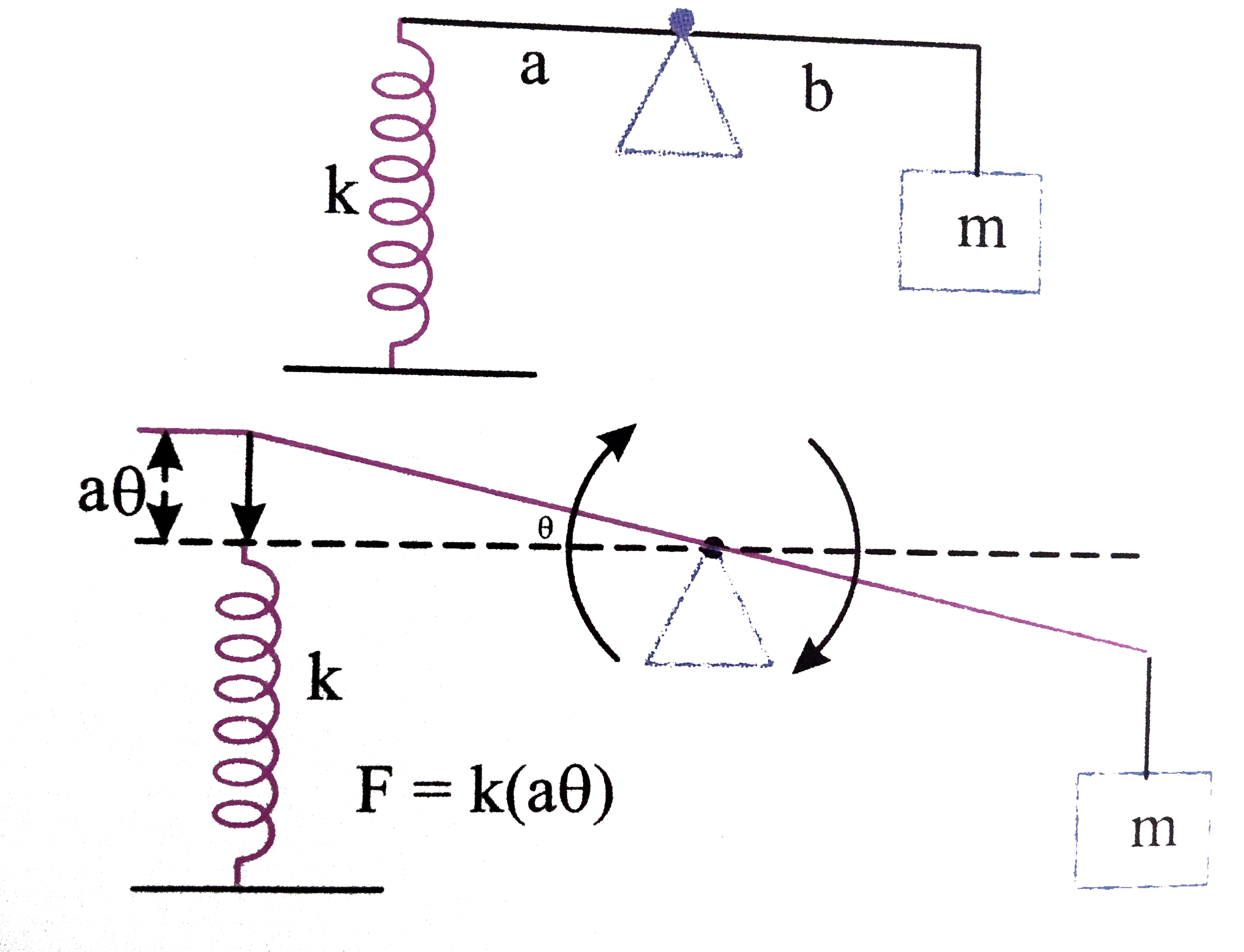
A small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

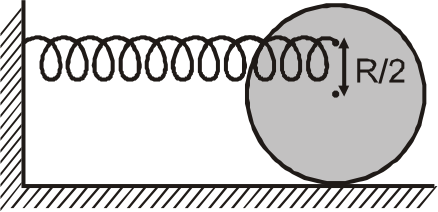
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionOne mass m is suspended from a spring. Time period of oscilation is T. now if spring is divided into n pieces & these are joined in parallel order then time period of oscillation if same mass is suspended.
View Solution

