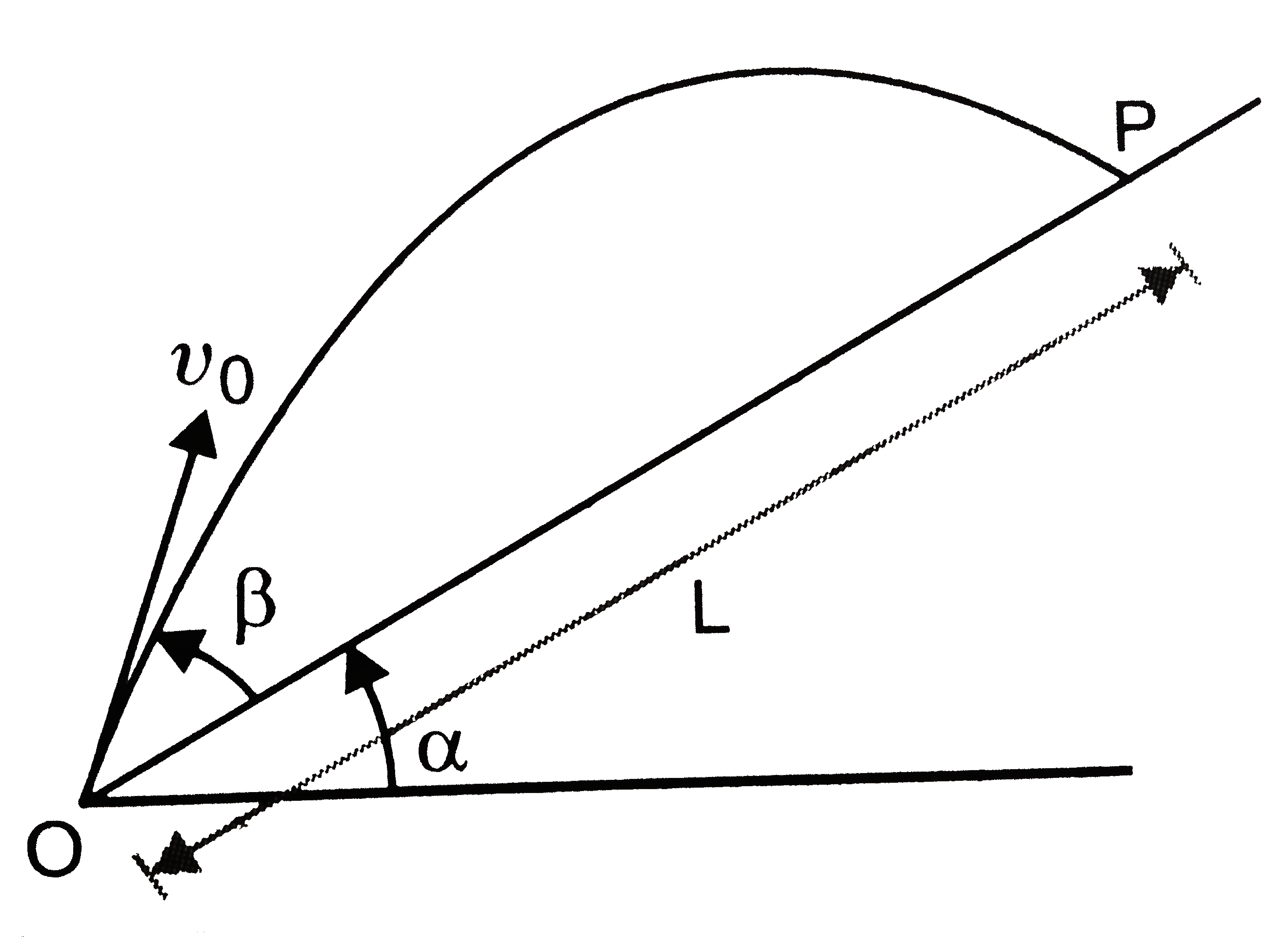
A particle is projected in air an angle to a surface which itself is inclined at an angle to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) at which range will be maximum.
The correct Answer is:C
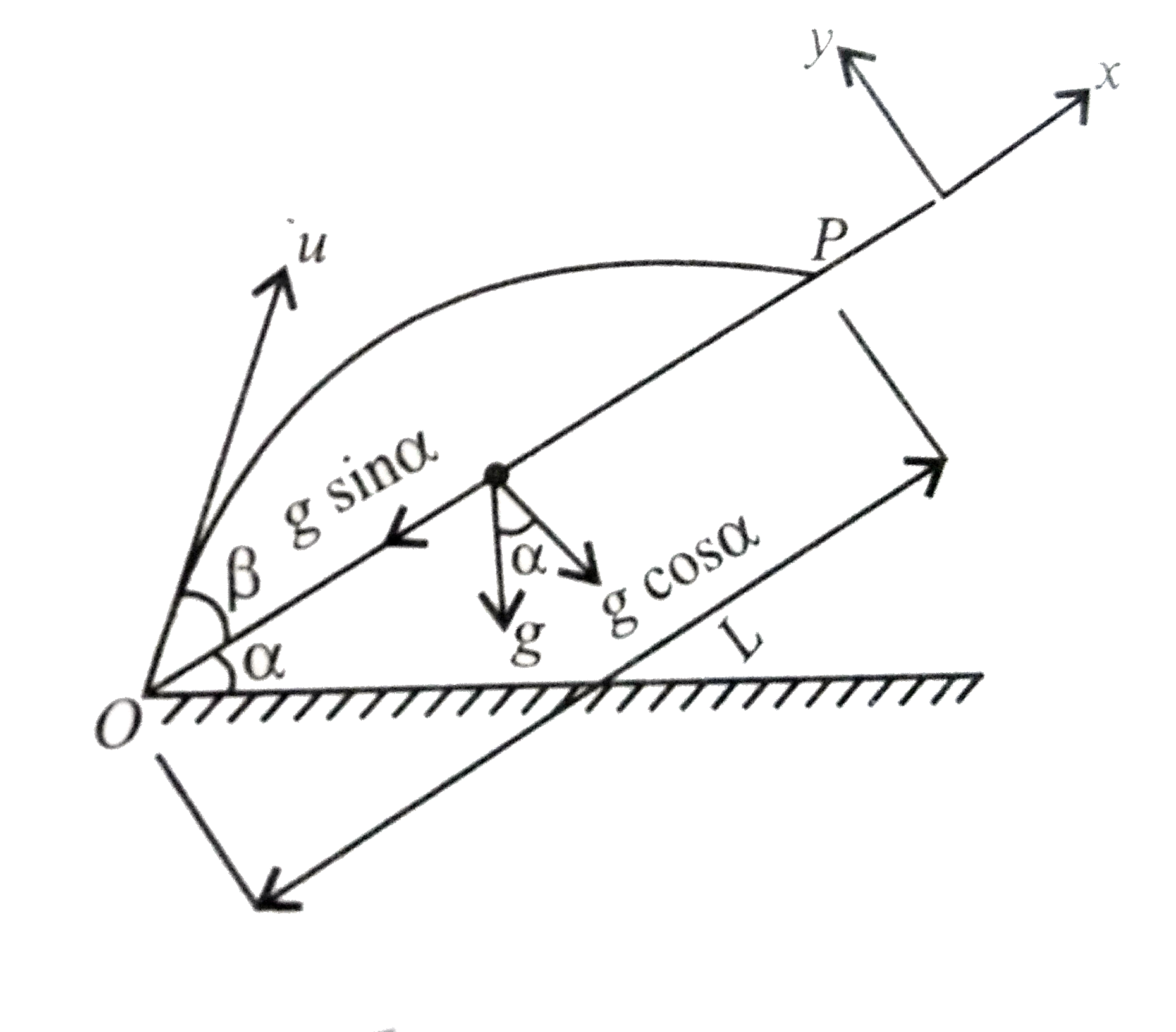
Take the x-axis along the incline and y-axis perpendicular to the plane.
When the particle lands at P its y coordinate becomes zero.
For motion along inclined plane,
Substituting the value of t from eq. (i), we get
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Uniform Circular Motion
14 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Miscellaneous Questions
14 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Relative Velocity In Two Dimensions
4 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.

View SolutionA particle is projected in aer an angle β to a surface which itself is inclined at an angle α to the horixonta (Fig. 2 (EP). 26)
(a) Find an ecxpression for range on the plane surface (distanc eon the plance from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.

View Solution
Knowledge Check
A particle I projected at an angle of elevation α after time t it makes an angle βwith horizontal. The velocity of projection is
A2gtcosβsin(α−β)Bgtcosβsin(α−β)Cgt2sin(α−β)D4gtsin(α−β)A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
Find the time taken by the particle to hit the plane.A34sB3sC4sD43sA particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
Acotβ=−tan(α−β)Bcotβ=2tan(α−β)Ccotα=tan(α−β)Dcotα=2tan(α−β)
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionThe ratio of the greatest range up an inclined plane through the point of projection and the distance through which a particle falls freely during the corresponding time of flight is
View SolutionA particle is projected at an angle with horizontal. If T is the time of flight and R is a horizontal range, then θ is
View Solution
