A particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time and is zero when If the velocity of the particle is momentary zero when determine the acceleration a and the velocity v when
The correct Answer is:A, B
To solve the problem step by step, we will use the equations of motion under constant acceleration.
Step 1: Identify the known values
- Initial displacement s0=2m at t=0s
- Displacement s=0m at t=10s
- Velocity v=0 at t=6s
Step 2: Use the equation of motion for displacement
The equation of motion for displacement is given by:
s=s0+ut+12at2
At t=0:
s0=2m
At t=10s:
0=2+10u+12a(102)
This simplifies to:
0=2+10u+50a(1)
Step 3: Use the equation for velocity
The equation for velocity is:
v=u+at
At t=6s:
0=u+6a(2)
Step 4: Solve the equations simultaneously
From equation (2), we can express u in terms of a:
u=−6a
Now substitute u in equation (1):
0=2+10(−6a)+50a
This simplifies to:
0=2−60a+50a
0=2−10a
10a=2⟹a=0.2m/s2
Step 5: Find the initial velocity u
Substituting a back into equation (2):
u=−6(0.2)=−1.2m/s
Step 6: Find the velocity at t=10s
Using the velocity equation again:
v=u+at
Substituting u and a:
v=−1.2+0.2×10
v=−1.2+2=0.8m/s
Final Results
- Acceleration a=0.2m/s2
- Velocity at t=10s is v=0.8m/s
- Initial displacement s0=2m at t=0s
- Displacement s=0m at t=10s
- Velocity v=0 at t=6s
The equation of motion for displacement is given by:
s=s0+ut+12at2
At t=0:
s0=2m
At t=10s:
0=2+10u+12a(102)
This simplifies to:
0=2+10u+50a(1)
The equation for velocity is:
v=u+at
At t=6s:
0=u+6a(2)
From equation (2), we can express u in terms of a:
u=−6a
Now substitute u in equation (1):
0=2+10(−6a)+50a
This simplifies to:
0=2−60a+50a
0=2−10a
10a=2⟹a=0.2m/s2
Substituting a back into equation (2):
u=−6(0.2)=−1.2m/s
Using the velocity equation again:
v=u+at
Substituting u and a:
v=−1.2+0.2×10
v=−1.2+2=0.8m/s
- Acceleration a=0.2m/s2
- Velocity at t=10s is v=0.8m/s
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
The velocity of a particle is zero at time t = 2s, then
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionIf s=4t+1t is the equation o motion of a particle, then the acceleration when velocity vanishes, is
View SolutionA constant force acts on a particle and its displacement x (in cm) is related to the time t (in s) by the equation t=√x+3, when the velocity of the particle is zero, its displacement ( in cm) is
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
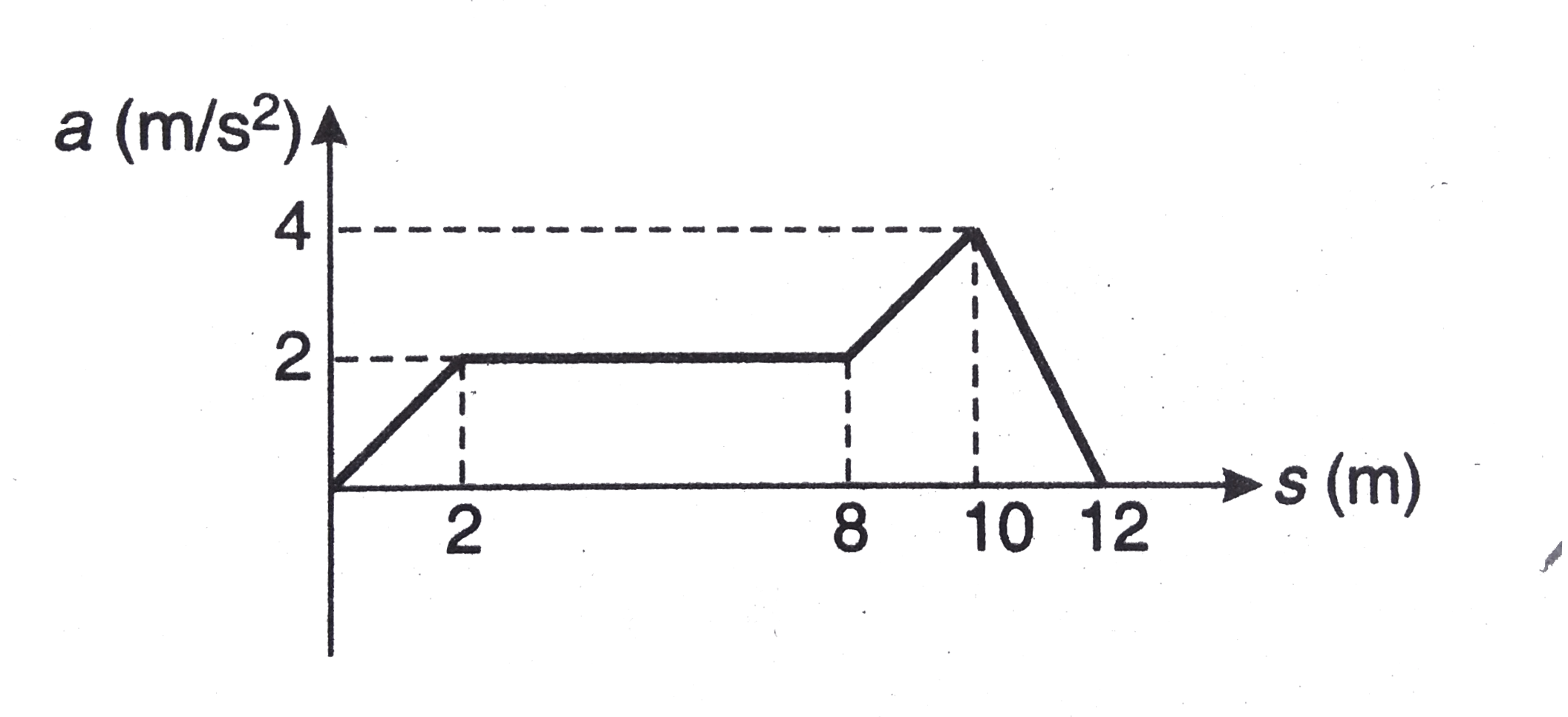
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View Solution
