A pendulum of mass 1 kg and length = 1m is released from rest at angle = 60º. The power delivered by all the forces acting on the bob at angle = 30º will be: (g = 10 m/s2)
13.4 W
20.4 W
24.6 W
zero
The correct Answer is:A
To solve the problem of finding the power delivered by all the forces acting on the bob of a pendulum at an angle of 30∘, we can follow these steps:
Step 1: Identify the Given Data
- Mass of the pendulum bob, m=1kg
- Length of the pendulum, ℓ=1m
- Initial angle, θ1=60∘
- Angle at which we want to find the power, θ2=30∘
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the Change in Height
To find the change in potential energy, we first need to calculate the height of the bob at both angles.
- Height at 60∘:
h1=ℓ−ℓcos(60∘)=1−1⋅12=0.5m
- Height at 30∘:
h2=ℓ−ℓcos(30∘)=1−1⋅√32=1−0.866=0.134m
Step 3: Calculate the Change in Potential Energy
The change in potential energy (ΔPE) from 60∘ to 30∘ is given by:
ΔPE=mgh1−mgh2=mg(h1−h2)
Substituting the values:
ΔPE=1⋅10⋅(0.5−0.134)=10⋅0.366=3.66J
Step 4: Calculate the Velocity at 30∘
Using the conservation of energy, the change in potential energy is equal to the change in kinetic energy. Thus:
ΔKE=12mv2=ΔPE
12⋅1⋅v2=3.66
v2=2⋅3.66=7.32
v=√7.32≈2.71m/s
Step 5: Calculate the Force Acting on the Bob at 30∘
The force acting on the bob due to gravity at 30∘ is:
F=mgsin(30∘)=1⋅10⋅12=5N
Step 6: Calculate the Power Delivered by the Forces
The power (P) delivered by the forces acting on the bob is given by:
P=F⋅v
Substituting the values:
P=5⋅2.71≈13.55W
Final Answer
The power delivered by all the forces acting on the bob at an angle of 30∘ is approximately 13.55W.
---
- Mass of the pendulum bob, m=1kg
- Length of the pendulum, ℓ=1m
- Initial angle, θ1=60∘
- Angle at which we want to find the power, θ2=30∘
- Acceleration due to gravity, g=10m/s2
To find the change in potential energy, we first need to calculate the height of the bob at both angles.
h1=ℓ−ℓcos(60∘)=1−1⋅12=0.5m
h2=ℓ−ℓcos(30∘)=1−1⋅√32=1−0.866=0.134m
The change in potential energy (ΔPE) from 60∘ to 30∘ is given by:
ΔPE=mgh1−mgh2=mg(h1−h2)
Substituting the values:
ΔPE=1⋅10⋅(0.5−0.134)=10⋅0.366=3.66J
Using the conservation of energy, the change in potential energy is equal to the change in kinetic energy. Thus:
ΔKE=12mv2=ΔPE
12⋅1⋅v2=3.66
v2=2⋅3.66=7.32
v=√7.32≈2.71m/s
The force acting on the bob due to gravity at 30∘ is:
F=mgsin(30∘)=1⋅10⋅12=5N
The power (P) delivered by the forces acting on the bob is given by:
P=F⋅v
Substituting the values:
P=5⋅2.71≈13.55W
The power delivered by all the forces acting on the bob at an angle of 30∘ is approximately 13.55W.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:JEE Advanced
Explore 24 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:More than One Option is Correct
Explore 13 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Subjective Questions
Explore 2 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
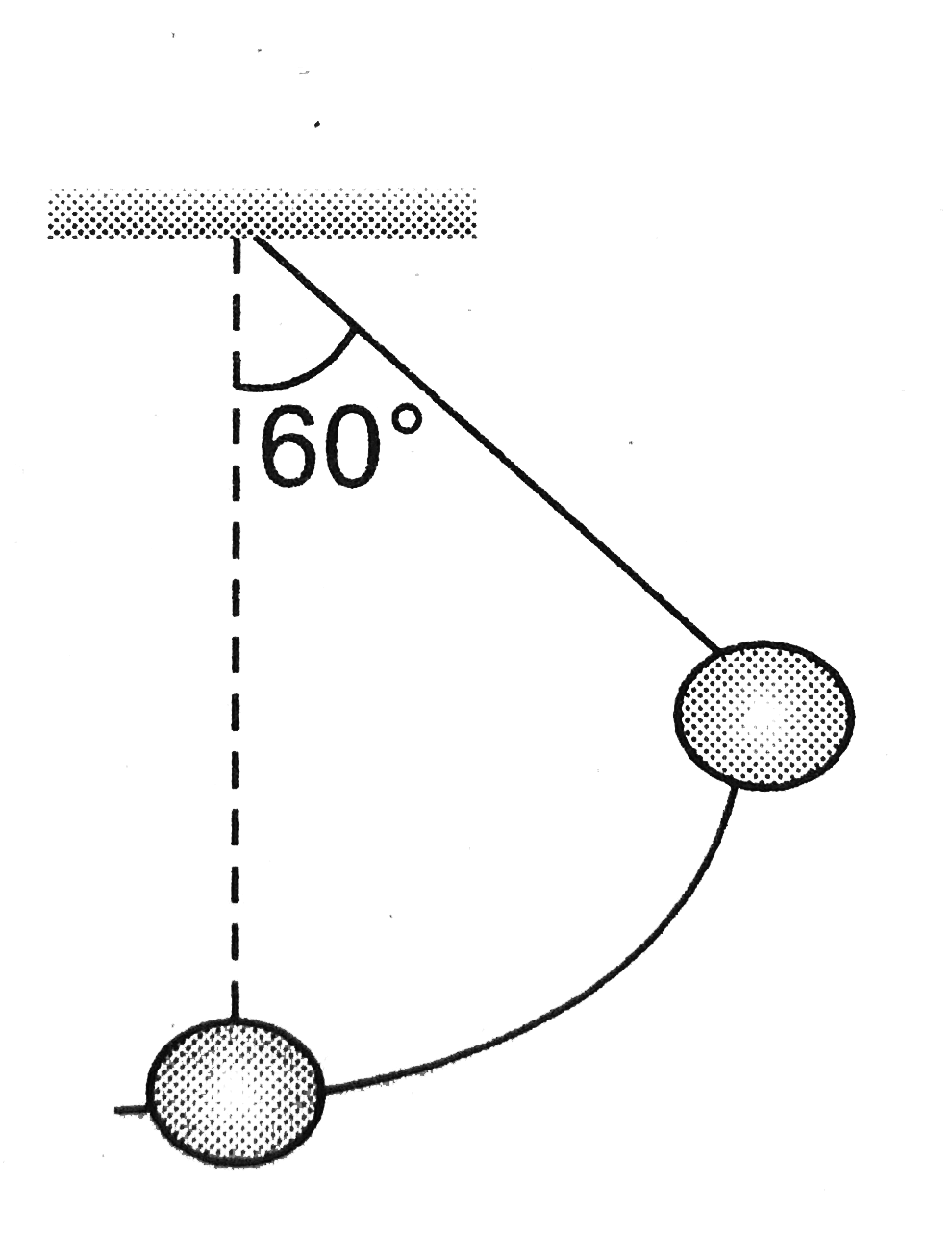
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionA body of mass m, accelerates uniformly from rest to V1 in time t1. The instantaneous power delivered to the body as a function of time t is.
View SolutionA particle of mass 1 kg moves in a circular path of radius 1 m such that its speed varies with time as per equation v=3t2m/s where time t is in seconds. The power delivered by the force acting on the paritcle at t=1s, is :−
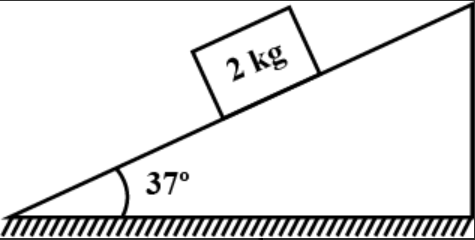
View SolutionA block of mass 2 kg rests on an inclined plane of inclination angle 37∘ , then calculate the force of friction acting on the block [ take g = 10m/s2)
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionA balloon os mass 2 KG is rising up with an acceleration of 4ms2 . The upward force acting on the balloon is (g = 10 ms^-2)
View SolutionA 5kg mass is accelerated from rest to 60 m/s in 1 sec. what force acts on it:
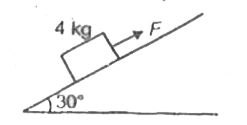
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View SolutionThe system is released from rest. All surface are smooth . Find the angle theta at which the acceleration of wedge is maximum. ( given .Mm=12)
View Solution