A person standing oin the floor of an elevator drops as coin. The coin reaches the floor of the elevator in a time t1 if the elevator is stationary and in the t2 if it is moving uniformly. Then
t1=t2
t1<t2
t1>t2
t1<t2ort1>t2 depending on whether the lift is going up or down.
The correct Answer is:A
To solve the problem, we need to analyze the situation of a coin being dropped in two different scenarios: when the elevator is stationary and when it is moving uniformly.
1. Understanding the Scenarios:
- Scenario 1: The elevator is stationary. When the person drops the coin, it falls under the influence of gravity. The time taken for the coin to reach the floor of the elevator is denoted as t1.
- Scenario 2: The elevator is moving uniformly (either upwards or downwards). The time taken for the coin to reach the floor of the elevator in this case is denoted as t2.
2. Applying the Equations of Motion:
- For the stationary elevator, we can use the second equation of motion:
h=12gt21
Rearranging gives:
t1=√2hg
- For the moving elevator, we consider that the elevator is moving with a constant velocity v. In this case, we can analyze it from the perspective of an observer inside the elevator. The coin is still falling under gravity, and the time taken to reach the floor is:
h=12gt22
Rearranging gives:
t2=√2hg
3. Comparing the Times:
- Since both equations for t1 and t2 yield the same expression:
t1=√2hgandt2=√2hg
- This shows that t1=t2.
4. Conclusion:
- Therefore, the time taken for the coin to reach the floor of the elevator is the same in both cases, regardless of whether the elevator is stationary or moving uniformly. The correct answer is that t1=t2.
Final Answer:
- t1=t2
- Scenario 1: The elevator is stationary. When the person drops the coin, it falls under the influence of gravity. The time taken for the coin to reach the floor of the elevator is denoted as t1.
- Scenario 2: The elevator is moving uniformly (either upwards or downwards). The time taken for the coin to reach the floor of the elevator in this case is denoted as t2.
- For the stationary elevator, we can use the second equation of motion:
h=12gt21
Rearranging gives:
t1=√2hg
h=12gt22
Rearranging gives:
t2=√2hg
- Since both equations for t1 and t2 yield the same expression:
t1=√2hgandt2=√2hg
- This shows that t1=t2.
- Therefore, the time taken for the coin to reach the floor of the elevator is the same in both cases, regardless of whether the elevator is stationary or moving uniformly. The correct answer is that t1=t2.
- t1=t2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples
11 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A person is standing at the floor of lift drops a coin The coin reaches the floor of lift in time t1. if elevator is stationary and in time t2, if it is moving uniformly then
View SolutionThe force exerted by the floor of an elevator on the foot of a person standing there is more than the weight of the person if the elevator is :
View Solution
Knowledge Check
A bolt of mass 0.2 kg falls from the ceiling of an elevator moving down with a uniform speed of 5ms−1. It hits the floor of the elevator (length of the elevator = 5 m) and does not rebound. The amount of heat produced by the impact is (Take g=10ms−2)
A5 JB10 JC15 JD20 J
An elevator is descending with uniform acceleration.To measure the acceleration, a person in the elevator drops a coin at momen the elevator strts. The coin is 6 ft asbove the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate these dta the acceleration of the elevator.
View Solution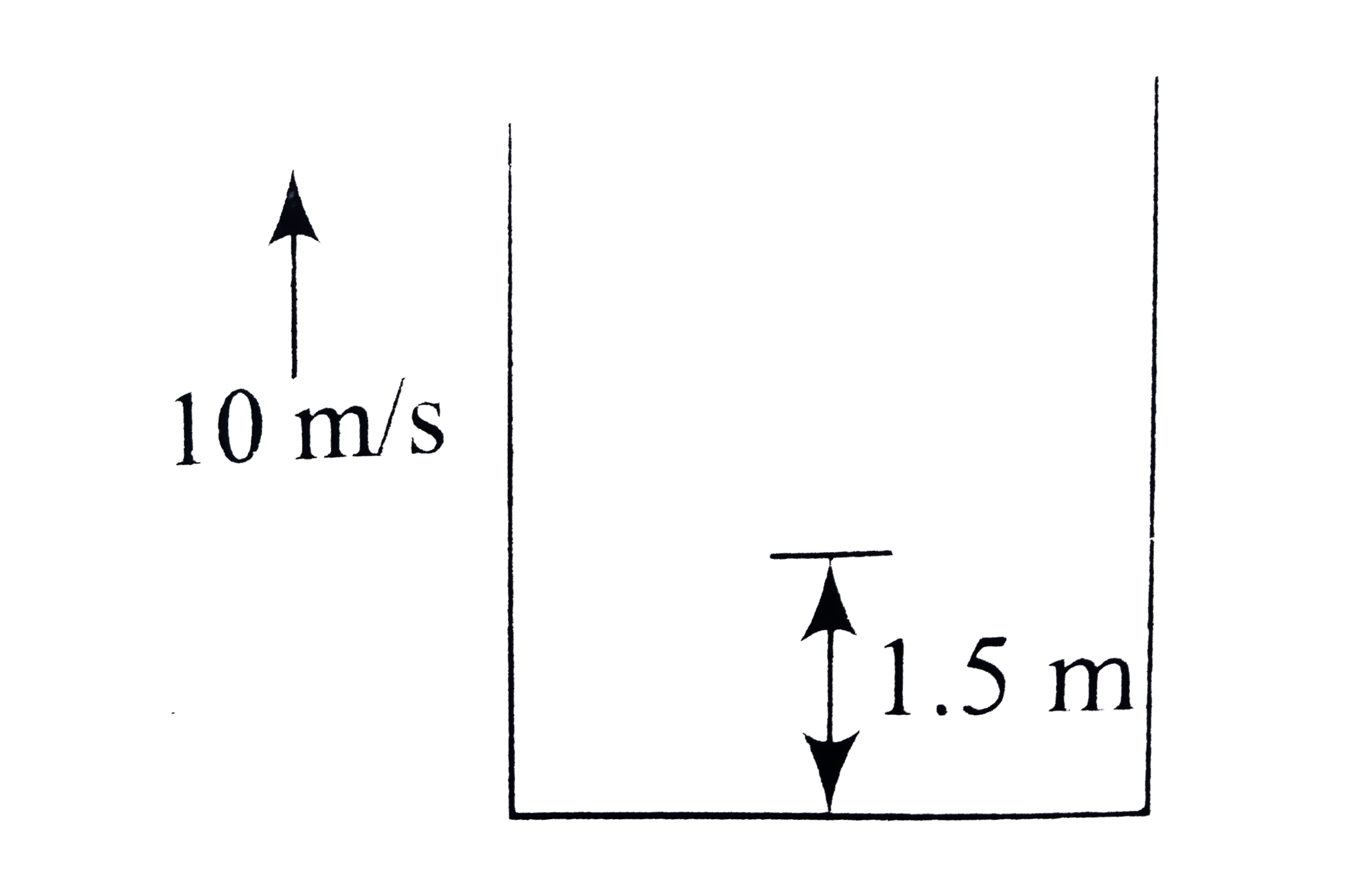
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View Solution
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the acceleration of the elevator in upward direction, (mss2):
View Solution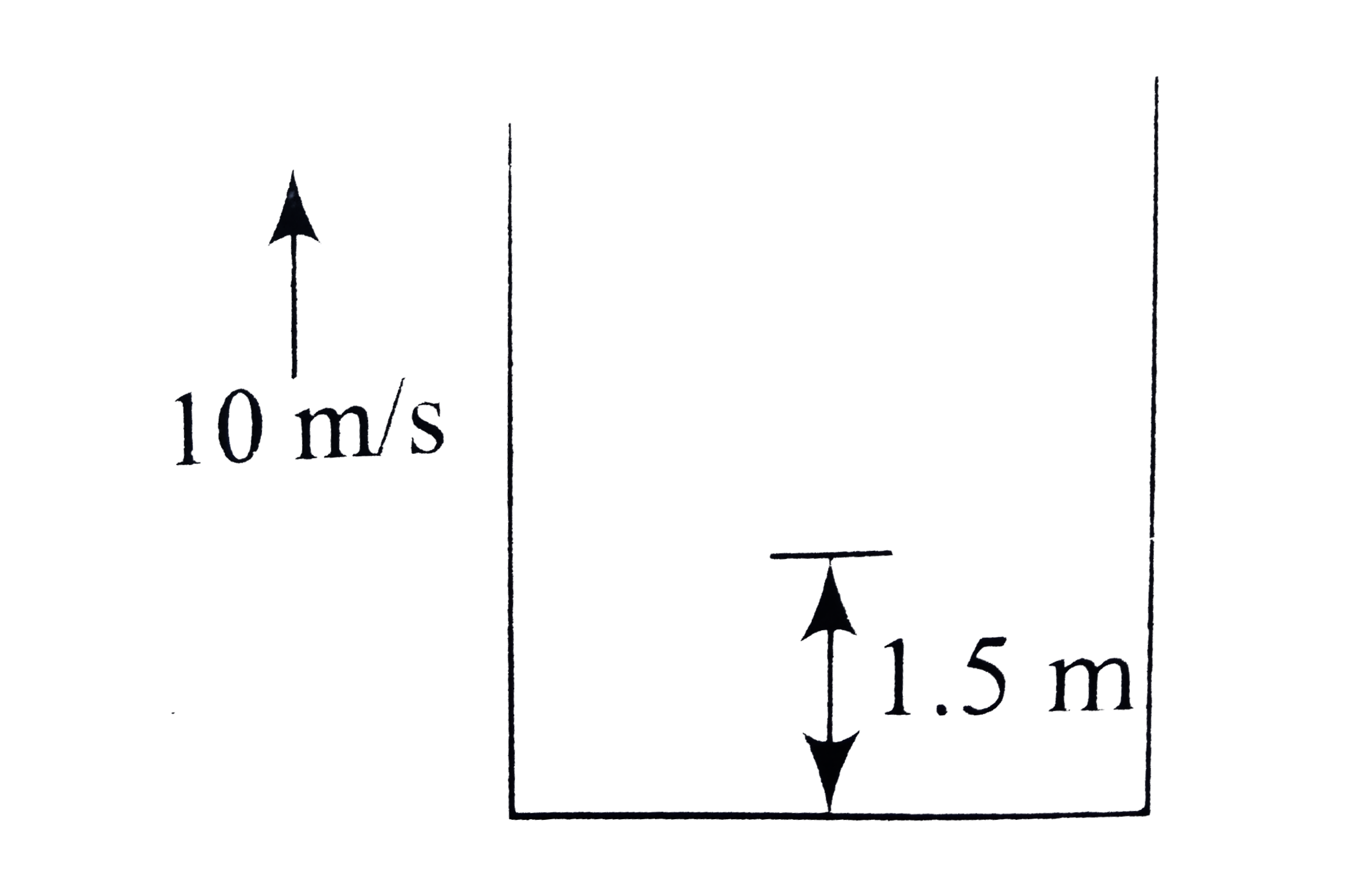
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:
View SolutionA man is standing on a weighing machine kept on the floor of an elevator. The ratio of measured weight of the man when elevator is at rest and when it is moving with downward acceleration a is 3 : 2. The value of a is :
View SolutionA ball of mass m is released from rest relative to elevator at a height h, above the floor of the elevator. After making collision with the floor of the elevator it rebounces to height h2. The coefficient of restitution for Collision is e. For this situation, mark the correct statement(s).

View SolutionA bob of mass 0.3 kg falls from the ceiling of an elevator moving down with a uniform speed of 7ms−1. If hits the floor of the elevator (length of the elevator = 3m) and does not rebound. What is the heat produced by the impact ? Would your answer be different if the elevator were stationary ?
View Solution
