In an imaginary atmosphere, the air exerts a small force F on any particle in the direction of the particle's motion. A particle of mass m projected upward takes time t1 and reaching the maximum height and t2 in the return journey to the original point. Then
t1<t2
t1>t2
t1=t2
the relation between t1andt2 depends n the mass of the particle.
The correct Answer is:B
To solve the problem, we need to analyze the motion of a particle projected upward in an imaginary atmosphere where a force F acts in the direction of the particle's motion. We will determine the time taken to reach the maximum height (t1) and the time taken to return to the original point (t2).
1. Identify Forces Acting on the Particle:
- When the particle is moving upward, the forces acting on it are:
- Gravitational force: mg (downward)
- Force F (upward)
- The net force when moving upward is:
Fnet=F−mg
- This results in an upward acceleration a:
ma=F−mg⟹a=F−mgm=Fm−g
2. Using the Equation of Motion for Upward Journey:
- The particle is projected with an initial velocity u and reaches the maximum height H in time t1.
- At maximum height, the final velocity v=0.
- Using the second equation of motion:
H=ut1+12at21
- Substituting a:
H=ut1+12(Fm−g)t21
3. Finding the Time t1:
- Rearranging the equation gives:
0=ut1+12(Fm−g)t21−H
- This is a quadratic equation in t1. Solving for t1 leads to:
t1=√2Hg−Fm
4. Analyzing the Downward Journey:
- When the particle is falling back down, the forces acting are:
- Gravitational force: mg (downward)
- Force F (also downward)
- The net force is:
Fnet=mg+F
- The downward acceleration a′ is:
ma′=mg+F⟹a′=g+Fm
5. Using the Equation of Motion for Downward Journey:
- The initial velocity at the start of the downward journey is 0 and the distance traveled is H.
- Using the second equation of motion:
H=0⋅t2+12a′t22
- This simplifies to:
H=12(g+Fm)t22
6. Finding the Time t2:
- Rearranging gives:
t2=√2Hg+Fm
7. Comparing t1 and t2:
- We have:
t1=√2Hg−Fmandt2=√2Hg+Fm
- Since g−Fm<g+Fm, it follows that:
t1>t2
Conclusion:
Thus, the time taken to reach the maximum height t1 is greater than the time taken to return to the original point t2:
t1>t2
- When the particle is moving upward, the forces acting on it are:
- Gravitational force: mg (downward)
- Force F (upward)
- The net force when moving upward is:
Fnet=F−mg
- This results in an upward acceleration a:
ma=F−mg⟹a=F−mgm=Fm−g
- The particle is projected with an initial velocity u and reaches the maximum height H in time t1.
- At maximum height, the final velocity v=0.
- Using the second equation of motion:
H=ut1+12at21
- Substituting a:
H=ut1+12(Fm−g)t21
- Rearranging the equation gives:
0=ut1+12(Fm−g)t21−H
- This is a quadratic equation in t1. Solving for t1 leads to:
t1=√2Hg−Fm
- When the particle is falling back down, the forces acting are:
- Gravitational force: mg (downward)
- Force F (also downward)
- The net force is:
Fnet=mg+F
- The downward acceleration a′ is:
ma′=mg+F⟹a′=g+Fm
- The initial velocity at the start of the downward journey is 0 and the distance traveled is H.
- Using the second equation of motion:
H=0⋅t2+12a′t22
- This simplifies to:
H=12(g+Fm)t22
- Rearranging gives:
t2=√2Hg+Fm
- We have:
t1=√2Hg−Fmandt2=√2Hg+Fm
- Since g−Fm<g+Fm, it follows that:
t1>t2
Thus, the time taken to reach the maximum height t1 is greater than the time taken to return to the original point t2:
t1>t2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples
11 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time t(<T) will be
View SolutionThe height reached in time t by a particle thrown upward with a speed u is given by
h=ut−12gt2
where g=9.8ms2 is a constant. Find the time taken in reaching the maximum height.
View Solution
Knowledge Check
A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
Ag(t−T)2BH−12g(t−T)2C12g(t−T)2DH−g(t−T)2The motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
AmgBμtC2mgD2μt
A particle is thrown up vertically with a speed v1 in air . If takes time t1 in upward journey and t2(>t1) in the downward journey and returns to the starting point with a speed v2. Then:-
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
View SolutionTwo particles of equal mass are projected simultaneously with speeds 20m/s end 10√3m/s as shown in figure. Find the maximum height reached by the centre of mass of the particles
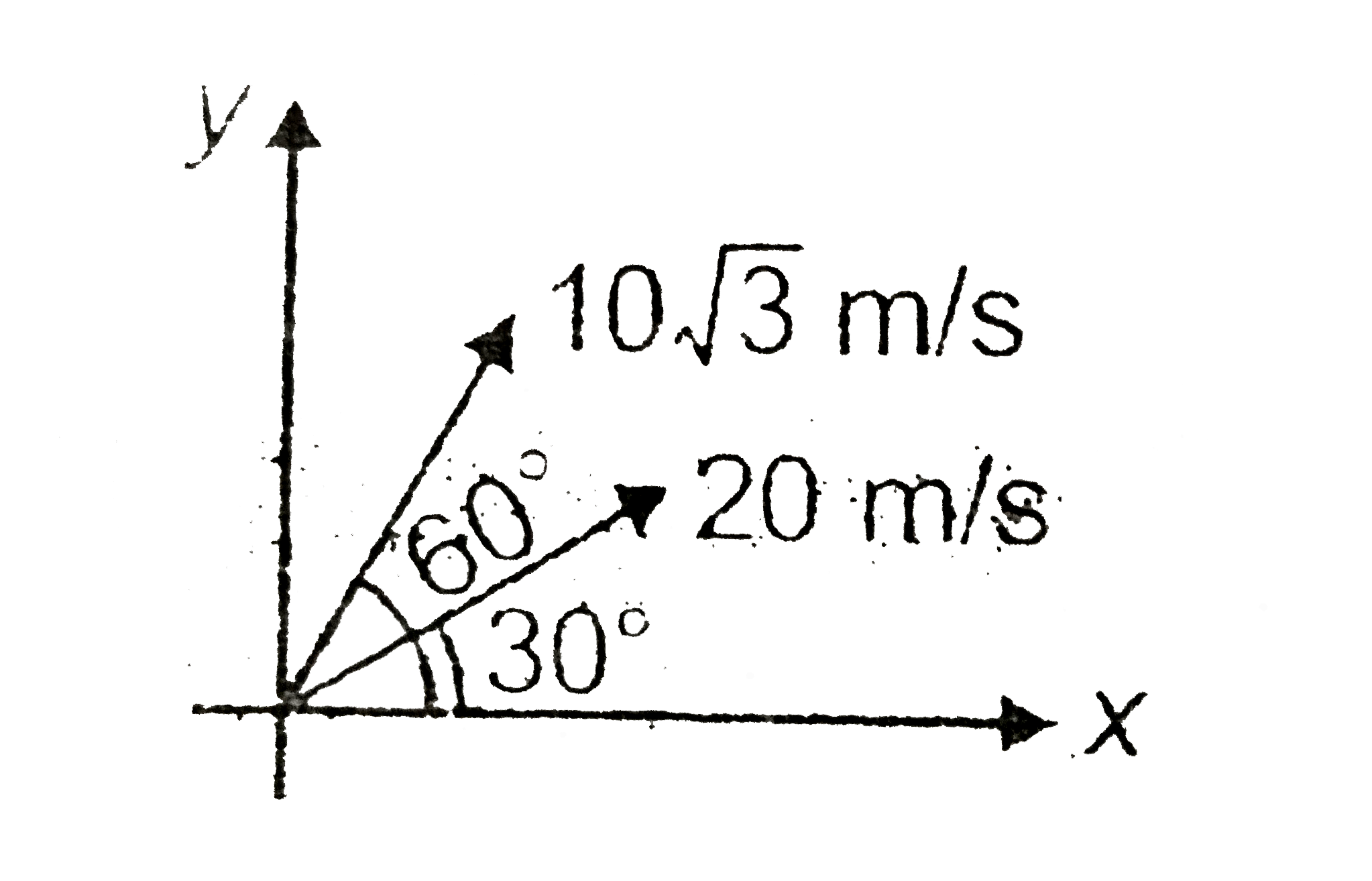
View SolutionThe motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
View Solution
