A positively charged particle having charge q1=1C and mass m1=40gm is revolving along a circle of radius R=40cm with velocity v1=5ms−1 in a uniform magnetic field with center of circle at origin O of a three-dimensional system. At t=0, the particle was at (0, 0.4m, 0) and velocity was directed along positive x direction. Another particle having charge q2=1C and mass m2=10g moving uniformly parallel to positive z-direction with velocity v2=40/πms−1 collides with revolving particle at t=0 and gets stuck to it. Neglecting gravitational force and coulomb force, calculate x-, y- and z-coordinates of the combined particle at t=π/40s.
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the initial conditions
- The first particle has:
- Charge q1=1C
- Mass m1=40g=0.04kg
- Velocity v1=5m/s
- Radius of circular motion R=40cm=0.4m
- Initial position at (0,0.4,0)
- The second particle has:
- Charge q2=1C
- Mass m2=10g=0.01kg
- Velocity v2=40πm/s in the positive z-direction.
Step 2: Calculate the velocity of the combined particle after collision
Using the conservation of momentum:
(m1+m2)⋅v=m1⋅v1+m2⋅v2
Where:
- v is the velocity of the combined particle after the collision.
- The initial velocity of the first particle is along the x-axis, so v1=5^i.
- The second particle's velocity is along the z-axis, so v2=40π^k.
Substituting the values:
(0.04+0.01)v=0.04⋅5^i+0.01⋅40π^k
0.05v=0.2^i+0.4π^k
Now, solving for v:
v=0.2^i+0.4π^k0.05=4^i+8π^km/s
Step 3: Determine the radius of the helical path
The radius of the helix is given by:
Rhelix=(m1+m2)vx(q1+q2)vx
Where vx=4m/s.
Substituting the values:
Rhelix=(0.04+0.01)⋅4(1+1)⋅4=0.05⋅42⋅4=0.28=0.025m
Step 4: Calculate the coordinates at t=π40s
1. X-coordinate: The x-coordinate will be equal to the radius of the helix:
x=Rhelix=0.025m
2. Y-coordinate: The y-coordinate remains constant since the motion is circular in the x-y plane:
y=Rhelix=0.025m
3. Z-coordinate: The z-coordinate changes uniformly with time:
z=vz⋅t=(8π)⋅(π40)=840=0.2m
Final Coordinates
Thus, the coordinates of the combined particle at t=π40s are:
(x,y,z)=(0.025,0.025,0.2)
- The first particle has:
- Charge q1=1C
- Mass m1=40g=0.04kg
- Velocity v1=5m/s
- Radius of circular motion R=40cm=0.4m
- Initial position at (0,0.4,0)
- Charge q2=1C
- Mass m2=10g=0.01kg
- Velocity v2=40πm/s in the positive z-direction.
Using the conservation of momentum:
(m1+m2)⋅v=m1⋅v1+m2⋅v2
- v is the velocity of the combined particle after the collision.
- The initial velocity of the first particle is along the x-axis, so v1=5^i.
- The second particle's velocity is along the z-axis, so v2=40π^k.
(0.04+0.01)v=0.04⋅5^i+0.01⋅40π^k
0.05v=0.2^i+0.4π^k
v=0.2^i+0.4π^k0.05=4^i+8π^km/s
The radius of the helix is given by:
Rhelix=(m1+m2)vx(q1+q2)vx
Where vx=4m/s.
Rhelix=(0.04+0.01)⋅4(1+1)⋅4=0.05⋅42⋅4=0.28=0.025m
1. X-coordinate: The x-coordinate will be equal to the radius of the helix:
x=Rhelix=0.025m
y=Rhelix=0.025m
z=vz⋅t=(8π)⋅(π40)=840=0.2m
Thus, the coordinates of the combined particle at t=π40s are:
(x,y,z)=(0.025,0.025,0.2)
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
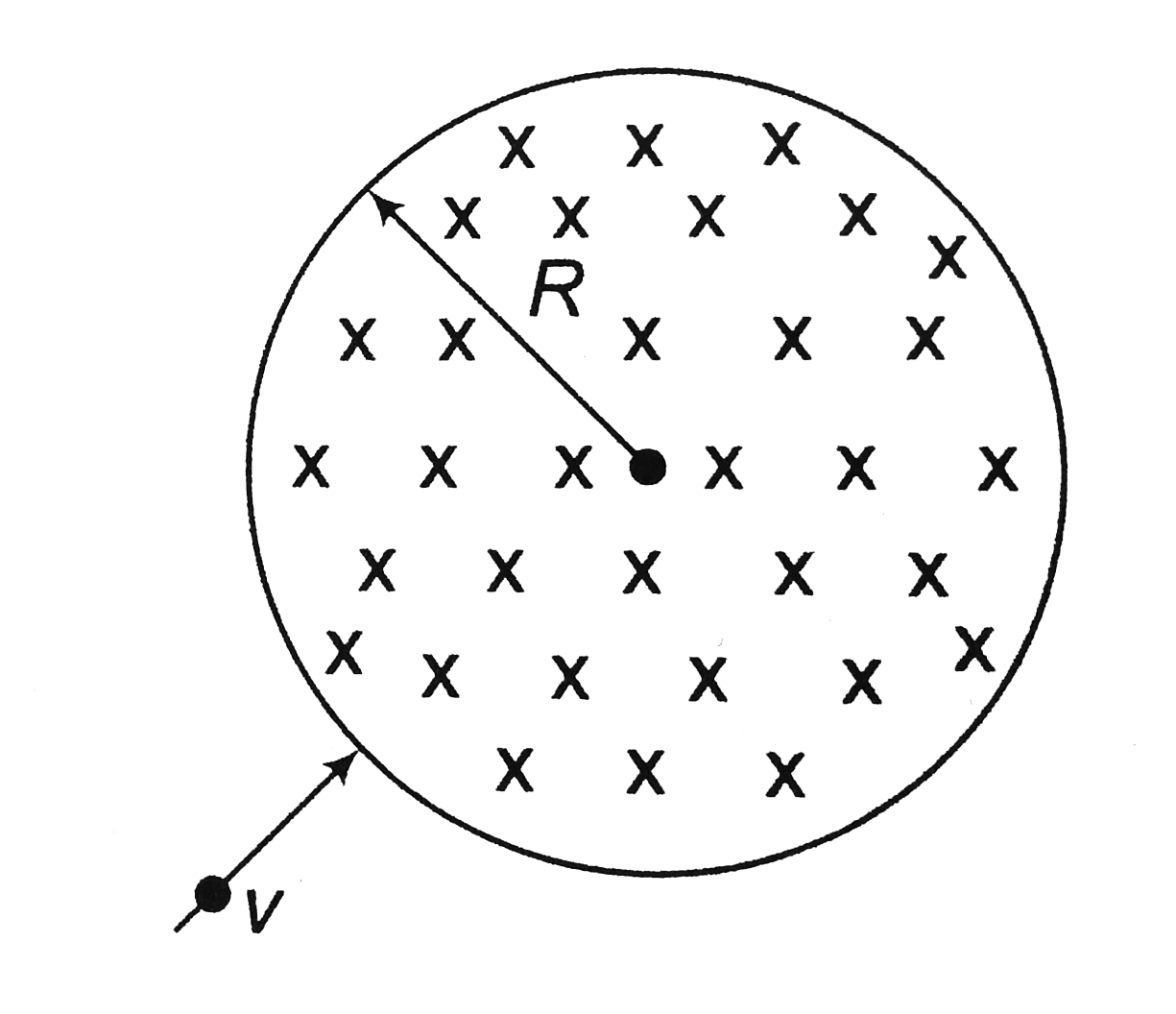
A particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
View SolutionA particle having a charge of 10.0μC and mass 1μg moves in a circle of radius 10 cm under the influence of a magnetic field of induction 0.1T. When the particle is at a point P, a uniform electric field is switched on so that the particle starts moving along the tangent with a uniform velocity. The electric field is
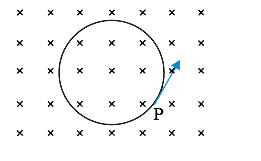
View SolutionA particle having charge of 20μC and mass 20μg moves along as circle of radius 5cm under the action of a magnetif field B=0.1 tesla. When the particle is at P, uniform transverse electric field is switched on an it is found that the particle continues along the tangent with a uniform velocity. Find the electric field

View SolutionA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

View SolutionA particle having a charge20μC and mass 20μg moves along a circle of radius 5.0 cm under the action of a magnetic field 5.0 cm under the action of a magnetic field B = 1.0 T. When the particle is at a point P, a uniform electric field is switched on and it is found that the particla continues on the tangent through P qith a uniform velocity. Find the electric field.
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View Solution
