A ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
The correct Answer is:C
To solve the problem step by step, we will use Snell's law and the relationship between the angles of incidence and refraction.
1. Understanding the Problem:
- A ray of light is passing from vacuum (refractive index μ1=1) into a medium with refractive index n.
- The angle of incidence i is twice the angle of refraction r. Therefore, we can express this relationship as:
i=2r
2. Applying Snell's Law:
- Snell's law states that:
μ1sin(i)=μ2sin(r)
- Substituting the values we have:
1⋅sin(i)=n⋅sin(r)
- This simplifies to:
sin(i)=n⋅sin(r)
3. Substituting the Relationship Between Angles:
- Since i=2r, we can substitute i in the equation:
sin(2r)=n⋅sin(r)
4. Using the Double Angle Formula:
- We can use the double angle formula for sine:
sin(2r)=2sin(r)cos(r)
- Substituting this into our equation gives:
2sin(r)cos(r)=n⋅sin(r)
5. Dividing by sin(r):
- Assuming sin(r)≠0, we can divide both sides by sin(r):
2cos(r)=n
6. Finding the Angle of Incidence:
- Rearranging gives:
cos(r)=n2
- Now, we can find r using the inverse cosine function:
r=cos−1(n2)
- Since i=2r, we substitute for r:
i=2cos−1(n2)
Final Answer:
The angle of incidence i is:
i=2cos−1(n2)
---
- A ray of light is passing from vacuum (refractive index μ1=1) into a medium with refractive index n.
- The angle of incidence i is twice the angle of refraction r. Therefore, we can express this relationship as:
i=2r
- Snell's law states that:
μ1sin(i)=μ2sin(r)
- Substituting the values we have:
1⋅sin(i)=n⋅sin(r)
- This simplifies to:
sin(i)=n⋅sin(r)
- Since i=2r, we can substitute i in the equation:
sin(2r)=n⋅sin(r)
- We can use the double angle formula for sine:
sin(2r)=2sin(r)cos(r)
- Substituting this into our equation gives:
2sin(r)cos(r)=n⋅sin(r)
- Assuming sin(r)≠0, we can divide both sides by sin(r):
2cos(r)=n
- Rearranging gives:
cos(r)=n2
- Now, we can find r using the inverse cosine function:
r=cos−1(n2)
- Since i=2r, we substitute for r:
i=2cos−1(n2)
The angle of incidence i is:
i=2cos−1(n2)
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective
29 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
13 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A ray of light passes from glass, having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
View SolutionWhen a monochromatic light ray is incident on a medium of refracive indexμwith angle of incidence θ1,the angle of refraction is θr.if θi is changed slightly byΔθi,then the corresponding change in θrwill be-
View Solution
Knowledge Check
A ray of light passes through an equilateral prism (refractive index 1.5) such that angle of incidence is equal to angle of emergence and the latter is equal to 3/4th of the angle of prism. Calculate the angle of deviation.
A60∘B30∘C45∘D120∘
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionA ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40∘. If the angle of emergence is 60∘, calculate the angle of the prism.
View SolutionA ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium
A is….
View SolutionConsider a ray of light passing from one medium to another. If the angle of refraction is less than the angle of incidence, will the speed of light in the second medium be less or more than that in the first medium?
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
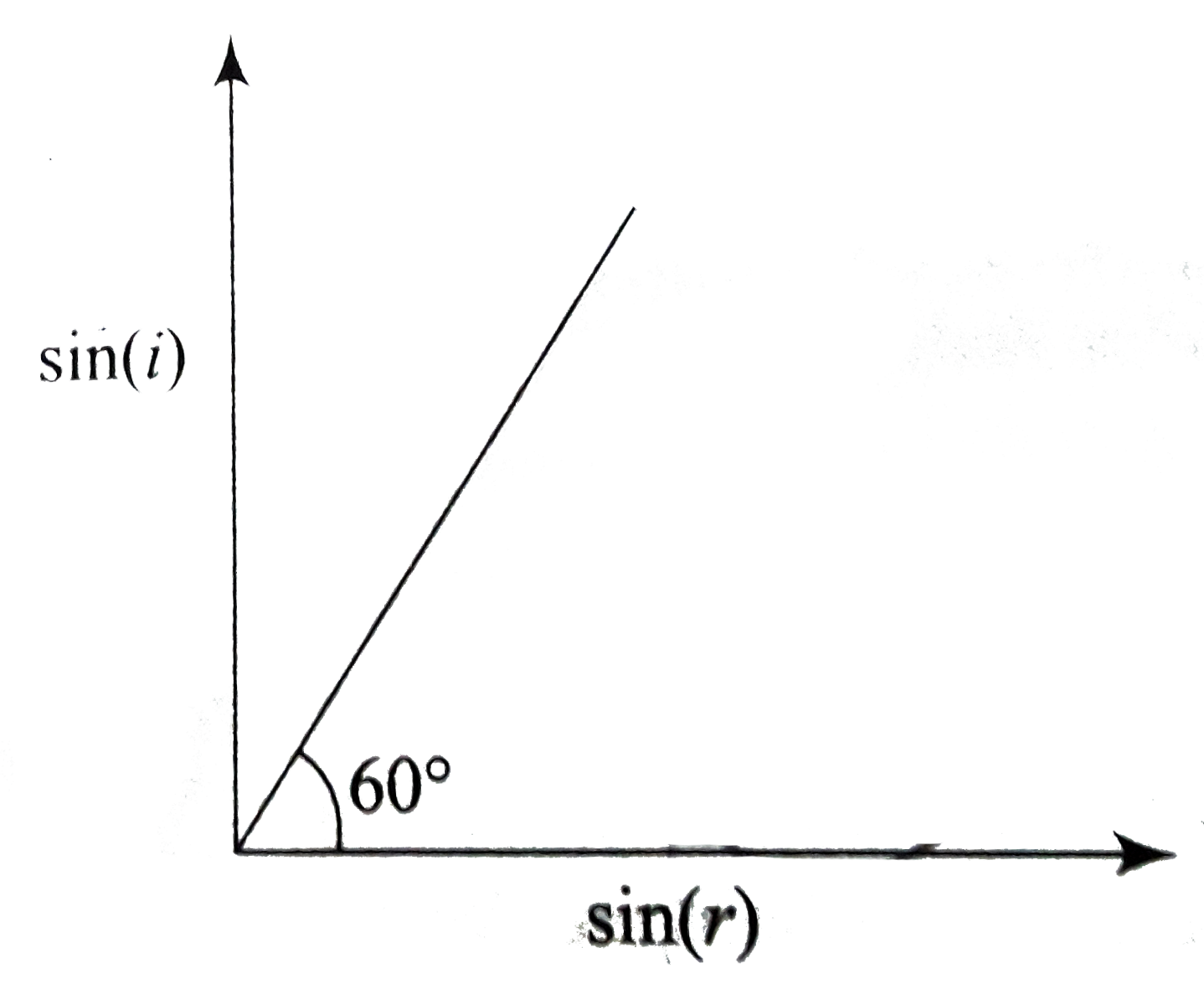
View Solution
