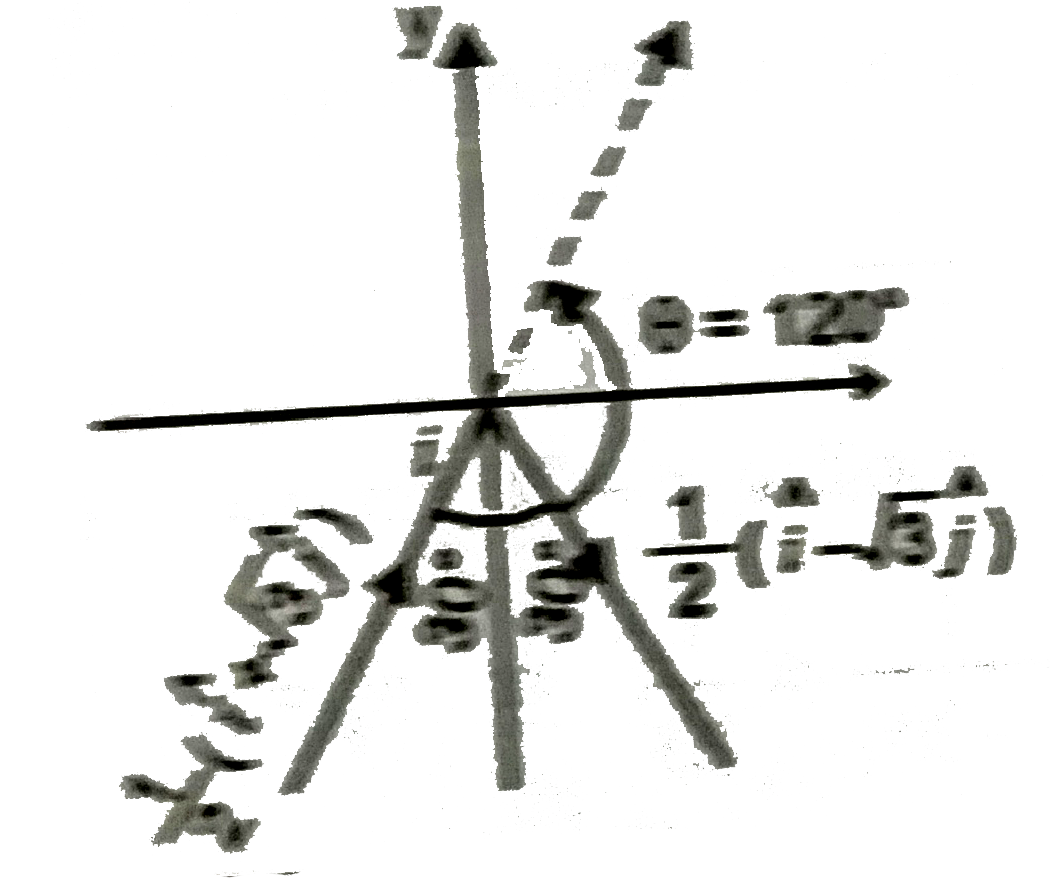
A ray of light travelling in the direction 12(ˆi+√3ˆj) is incident on a plane mirror. After reflection, it travels along the direction 12(ˆi−√3ˆj) . The anglel of incidence is
A
30∘
B
45∘
C
60∘
D
75∘
Video Solution
Text Solution
The correct Answer is:A
Here, →A=12(ˆi+√3ˆj)
and →B=12(ˆi−√3ˆj)
∴A=B=√I2+(√3)2=2 and →A.→B=−2
cosθ=→A.→BAB=−22×2=−12
θ=120∘, Fig.
Angle of incidence,
i=180∘−θ2=180∘−120∘2=30∘.
 .
.
|
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (Competition)Comprehension
7 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Integer Question
4 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (Exemplar) Multiple choice
16 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
Knowledge Check
A ray of light travelling in the direction 12(ˆi,+√3ˆj) is incident on a plane mirror. After reflection, it travels along the direction (1)/(2)(hati-sqrt3hatj) . The angle of incidence is
A30degreeB60degreeC45degreeD75degreeA ray of light travelling in the direction 12(ˆi+√3ˆj) is incident on a plane mirror. After reflectiion, it travels along the direction 12(ˆi+√3ˆj). The angle of incidence is
A30∘B45∘C60∘D75∘The expression (1√2ˆi+1√2ˆj) is a
AUnit vectorBNull vectorCVector of magnitude sqrt(2)DScalar
Let the x-z plane be the boundary between two transparent media. Medium 1 in z≥0 has a refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk is incident on the plane of separation. The angle of refraction in medium 2 is:
View SolutionFind the component of a vector →A=3ˆI+4ˆj along the direction of 2ˆI−3ˆj.
View SolutionThe component of vector A=2ˆi+3ˆj along the vector ˆi+ˆj is
View SolutionThe direction cosines of a vector ˆi+ˆj+√2ˆk are :
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View Solution
