A resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
increases continuously
decreases continuously
first decreases then increases
first increases then decreases
The correct Answer is:A
To solve the problem of finding the power consumed by a resistor R connected to a cell with an internal resistance of 5Ω, we will follow these steps:
Step 1: Understand the Circuit
The total resistance in the circuit is the sum of the external resistance R and the internal resistance of the cell, which is 5Ω. Therefore, the total resistance Rtotal can be expressed as:
Rtotal=R+5Ω
Step 2: Apply Ohm's Law
According to Ohm's Law, the current I flowing through the circuit can be calculated using the formula:
I=VRtotal
where V is the voltage of the cell.
Step 3: Substitute Total Resistance
Substituting the expression for Rtotal into the current equation, we get:
I=VR+5
Step 4: Calculate Power
The power P consumed by the resistor R can be calculated using the formula:
P=I2R
Substituting the expression for I from Step 3:
P=(VR+5)2R
This simplifies to:
P=V2R(R+5)2
Step 5: Analyze Power Variation
Now, we need to analyze how the power P changes as R varies from 1Ω to 5Ω. Since P is a function of R:
P(R)=V2R(R+5)2
We can observe that as R increases, the numerator V2R increases, while the denominator (R+5)2 also increases but at a slower rate initially.
Step 6: Conclusion
To conclude, as R increases from 1Ω to 5Ω, the power consumed by the resistor R will also increase continuously. Thus, the answer to the question is that the power consumed by R increases continuously as R varies from 1Ω to 5Ω.
The total resistance in the circuit is the sum of the external resistance R and the internal resistance of the cell, which is 5Ω. Therefore, the total resistance Rtotal can be expressed as:
Rtotal=R+5Ω
According to Ohm's Law, the current I flowing through the circuit can be calculated using the formula:
I=VRtotal
where V is the voltage of the cell.
Substituting the expression for Rtotal into the current equation, we get:
I=VR+5
The power P consumed by the resistor R can be calculated using the formula:
P=I2R
Substituting the expression for I from Step 3:
P=(VR+5)2R
This simplifies to:
P=V2R(R+5)2
Now, we need to analyze how the power P changes as R varies from 1Ω to 5Ω. Since P is a function of R:
P(R)=V2R(R+5)2
We can observe that as R increases, the numerator V2R increases, while the denominator (R+5)2 also increases but at a slower rate initially.
To conclude, as R increases from 1Ω to 5Ω, the power consumed by the resistor R will also increase continuously. Thus, the answer to the question is that the power consumed by R increases continuously as R varies from 1Ω to 5Ω.
Topper's Solved these Questions
Similar Questions
Statement I: When an external resistor of resistance R (connected across a cell to internal resistance r ) is varied, power consumed by resistance R is maximum when R = r.
Statement II: Power consumed by a resistor of constant resistance R is maximum when current through it is maximum.
View SolutionThe resistance of 0.1 N solution of acetic acid is 250 ohm whne measured ina cell of cell constant 250 ohm whne measured in acell of cell constant 1.15 cm−1 The equivalent conductance (inohm−1cm2equivalent−1) of 0.1 N acetic acid is
View SolutionFor the given circuit,
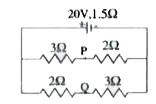
If internal resistance of cell is 1.5Ω, then
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What is the potential difference across the terminals of the cell?
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What would be the reading on the Ammeter?
View SolutionA cell of e.m.f. ε and internal resistance r sends a current of 1.0 A when it is connected to an external resistance of 1.9 Ω. But it sends a current of 0.5 A when it is connected to an resistance of 3.9Ω calculate the values of ε and r .
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
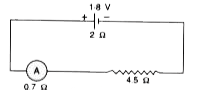
What would be the reading of the ammeter ?
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
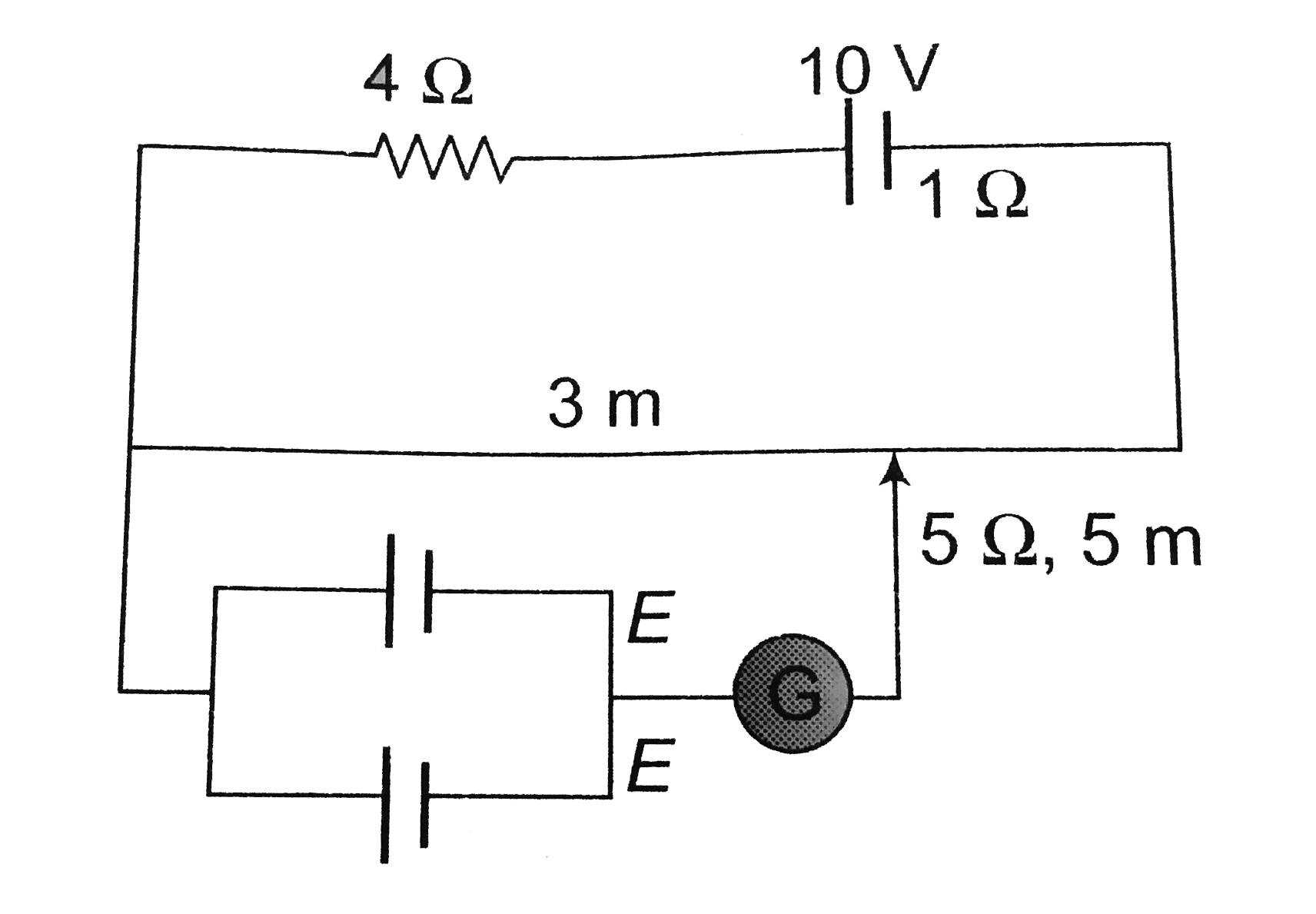
View SolutionA resistance of 4Ω and a wire of length 5 meters and resistance 5Ω are joined in series and connected to a cell of e.m.f. 10V and internal resistance 1Ω. A parallel combination of two identical cells is balanced across 300cm of wire. The e.m.f. E of each cell is
View Solution