A rigid large uniform square platform is resting on a flat horizontal ground supported at its vertices by four identical spring. At vertex l a wooden block, 6 cm high, is inserted below the spring. Calculate the change in height of the centre of the platform. Assume change in height to be small compared to dimension of the platform.
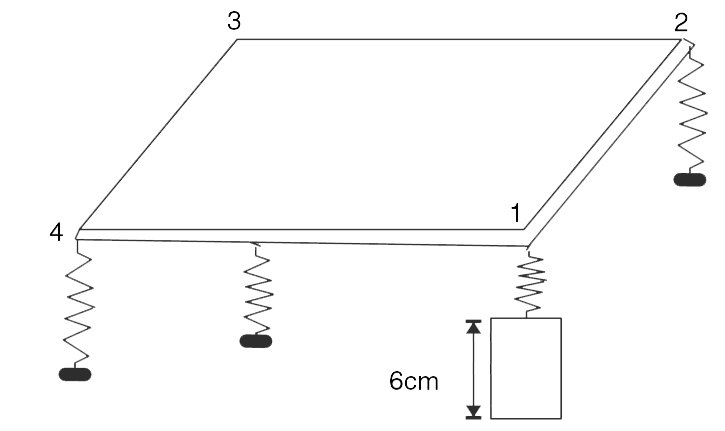
The correct Answer is:1.5cm
Topper's Solved these Questions
Similar Questions
A and B are two identical blocks of same mass 2 m and same physical dimensions as shown in figure −4.158 A is placed over the block B which is attached to one end of the spring of natural length l and spring contant k. The other end of the speing is attached to a wall. The system is resting on a smooth horizontal surface with the spring in the relaxed state. A small object of mass m moving horizontally with speed v at a height d above the horizontal surface hits the block B along the line of therir cntre of mass in a perfectly elastic collision. There is no friction between A and B.
Find the minimum value of v (sayvo)such that the block A will topple over block B.
What is the energy stored in the spring when the blocks A and B returns to their initial position as before collision

View SolutionOn a smooth horizontal platform a mass of 2 kg is dragged with a horizontal force of 10 Nt. On platform there are so many holes spreaded on its surface below which there is an air blower which exerts a force on block in upward direction depending on its height above the platformas →F=20(2−h)N, where h is the height of the block above the platform. Let at t=0 block starts from rest from origin of coordinate system shown. Find the equation of trajectory of the block during its motion. Consider x-axis along the motion ofparticle and y-axis in vertical up direction.
View Solution
Knowledge Check
Direction :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :A5.00×10−3sB1.00×10−2sC2.5×10−3sD1.00×10−3s
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed isAπ√L2g+√L4gsin−1(1)3Bπ4√Lg+√L4gsin−1(1)3Cπ√L2g+√L4gsin−1(2)3Dπ2√L2g+√L4gsin−1(2)3
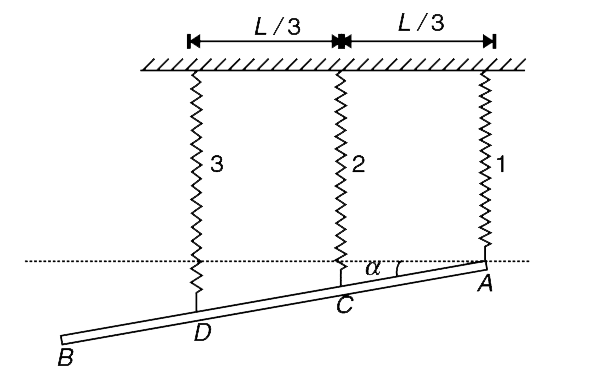
A uniform rod AB has mass M and length L. It is in equilibrium supported in vertical plane by three identical springs as shown in figure. The springs are connected at A, C and D such that AC=CD=L3. Assume that the springs are very stiff and the angle a made by the rod with the horizontal in equilibrium position is very small. (All springs are nearly vertical). Calculate the tension in the three springs.
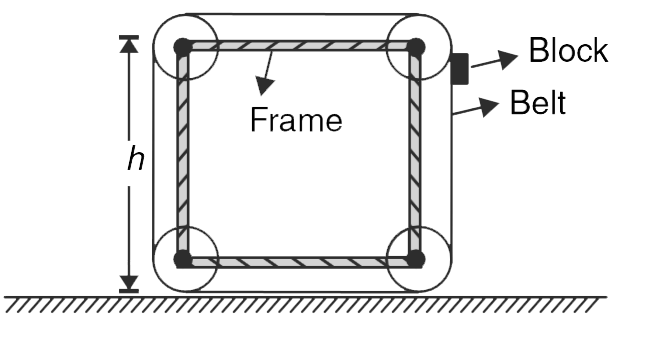
View SolutionA toy is made of a rectangular wooden frame with four small wheels at its vertices. A tight fitting belt of negligible mass runs around the frame passing over the wheels. Mass of the complete toy is M. Now a small block of mass m is stuck at the top of the right vertical segment of the belt and the system is released. Height of the toy is h. Find the speed of the block when it is about to hit the ground. Assume no slipping anywhere and neglect the dimension of the wheels
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :
View SolutionA block of mass 'm' is attached to a spring and is placed on a platform as shown in the figure, and the spring at this stage remains in a relaxed stage. When supporting platform is suddenly removed the mass begins to oscillate and moves down to a lowest position of 5 cm from its initial position. Then calculate the time taken by block to reach a height of 3 cm from its lowest position?

View SolutionA block of mass 'm' is attached to a spring and is placed on a platform as shown in the figure, and the spring at this stage remains in a relaxed stage. When supporting platform is suddenly removed the mass begins to oscillate and moves down to a lowest position of 5 cm from its initial position. Then calculate the time taken by block to reach a height of 3 cm from its lowest position?

View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is
View Solution
