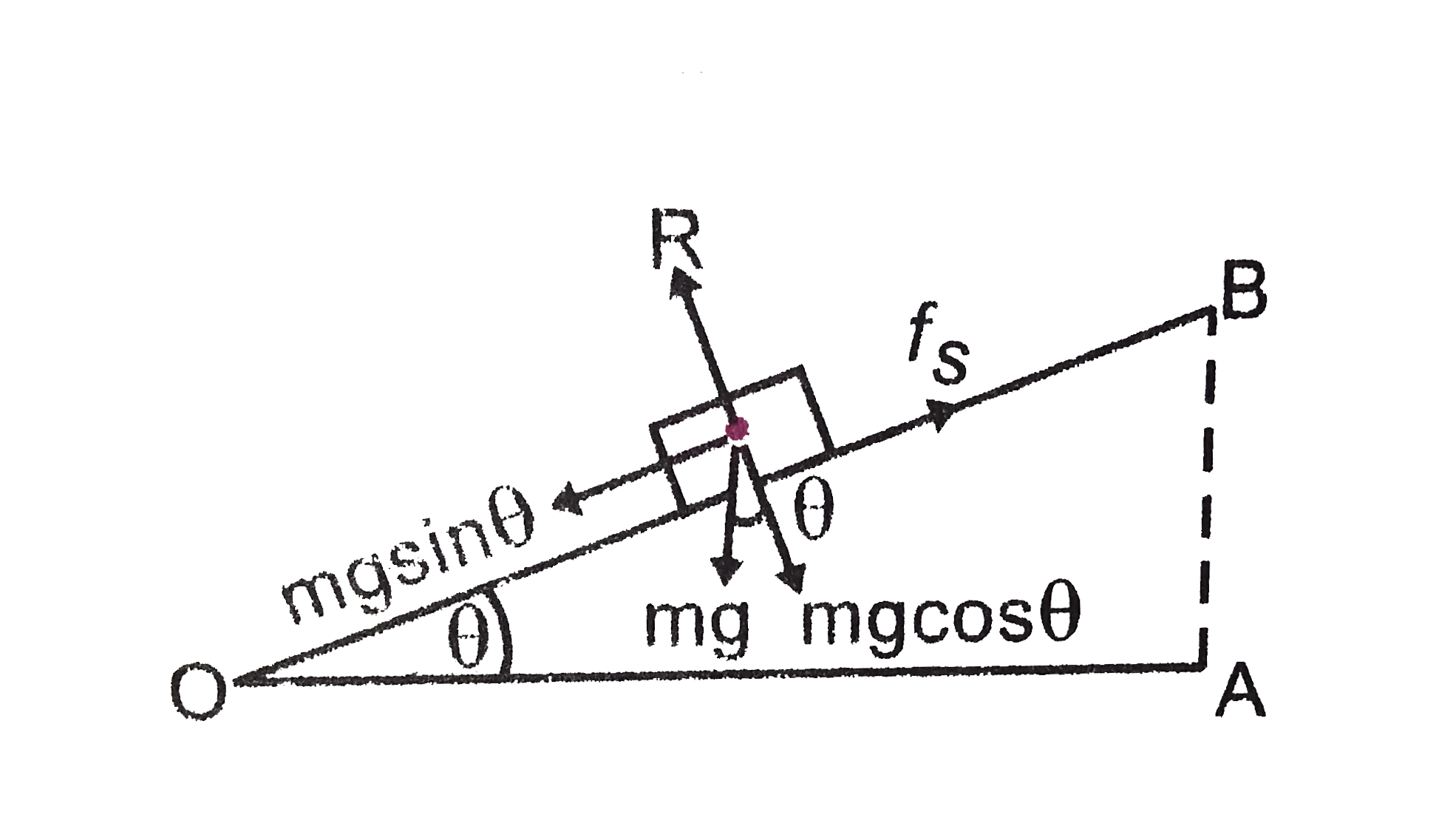
A rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the rocket, making an angle o with the horizontal, a point object of mass m is kept. The maximum coefficient of friction between the mass and the inclined surface such that the mass does not move is
tan2θ
tanθ
3tanθ
2tanθ
To solve the problem, we need to analyze the forces acting on the mass on the inclined plane inside the rocket. The rocket is accelerating upwards with an acceleration of 2g, where g is the acceleration due to gravity.
1. Identify the Forces Acting on the Mass:
- The mass m experiences gravitational force downward, which is mg.
- Due to the rocket's upward acceleration of 2g, the effective gravitational force acting on the mass becomes 3g (since g+2g=3g).
- The normal force N acts perpendicular to the inclined plane.
2. Components of Forces:
- The gravitational force can be resolved into two components:
- Perpendicular to the inclined plane: 3mgcosθ
- Parallel to the inclined plane: 3mgsinθ
3. Frictional Force:
- The frictional force Ff that prevents the mass from sliding down the incline is given by:
Ff=μN
- Where μ is the coefficient of friction and N is the normal force.
4. Normal Force Calculation:
- The normal force N acting on the mass is equal to the perpendicular component of the effective gravitational force:
N=3mgcosθ
5. Setting Up the Equation:
- For the mass to remain at rest on the incline, the frictional force must be equal to or greater than the component of the gravitational force acting down the incline:
Ff≥3mgsinθ
- Substituting for Ff:
μN≥3mgsinθ
- Substituting for N:
μ(3mgcosθ)≥3mgsinθ
6. Simplifying the Equation:
- Dividing both sides by 3mg (assuming m≠0 and g≠0):
μcosθ≥sinθ
7. Finding Maximum Coefficient of Friction:
- Rearranging gives:
μ≥sinθcosθ
- This simplifies to:
μ≥tanθ
Final Answer:
The maximum coefficient of friction μ such that the mass does not move is:
μ=tanθ
- The mass m experiences gravitational force downward, which is mg.
- Due to the rocket's upward acceleration of 2g, the effective gravitational force acting on the mass becomes 3g (since g+2g=3g).
- The normal force N acts perpendicular to the inclined plane.
- The gravitational force can be resolved into two components:
- Perpendicular to the inclined plane: 3mgcosθ
- Parallel to the inclined plane: 3mgsinθ
- The frictional force Ff that prevents the mass from sliding down the incline is given by:
Ff=μN
- Where μ is the coefficient of friction and N is the normal force.
- The normal force N acting on the mass is equal to the perpendicular component of the effective gravitational force:
N=3mgcosθ
- For the mass to remain at rest on the incline, the frictional force must be equal to or greater than the component of the gravitational force acting down the incline:
Ff≥3mgsinθ
- Substituting for Ff:
μN≥3mgsinθ
- Substituting for N:
μ(3mgcosθ)≥3mgsinθ
- Dividing both sides by 3mg (assuming m≠0 and g≠0):
μcosθ≥sinθ
- Rearranging gives:
μ≥sinθcosθ
- This simplifies to:
μ≥tanθ
The maximum coefficient of friction μ such that the mass does not move is:
μ=tanθ
Topper's Solved these Questions
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE.
1 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE. (MULTIPAL-CHOICE QUESTION WITH ONE OR MORE THAN ONE CORRECT ANSWER)
3 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
1 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- SOUNDBOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
Similar Questions
A mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View Solution
Knowledge Check
A rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the tocket, making an angle θ with the horizontal, a point object of mass m is kept, the minimum coefficient of friction μmin between the mass and the inclined suface such that the mass does not move is:
A2tanθB3tanθCtanθDtan2θA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
A2 kgB4 kgC1.6 kgD2.5 kgA body of mass m slides down an inclined plane making an angle of 45∘ with the horizontal. If the coefficient of friction between the body and the plane be 0.3, the acceleration of the body is approximately equal to :
A0.22 gB0.30 gC0.49 gD0.70 g
An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m walks down the board. If the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of does not slide is:

View Solution
