A simple pendulum having a bob of mass m undergoes smasll oscillastions with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
Suppose the speed of the bob the angle θ is v. Using conservation of energy between the extreme position and the position with angle theta.
=12mv2=mgl(cosθ−cosθ0) ……….i
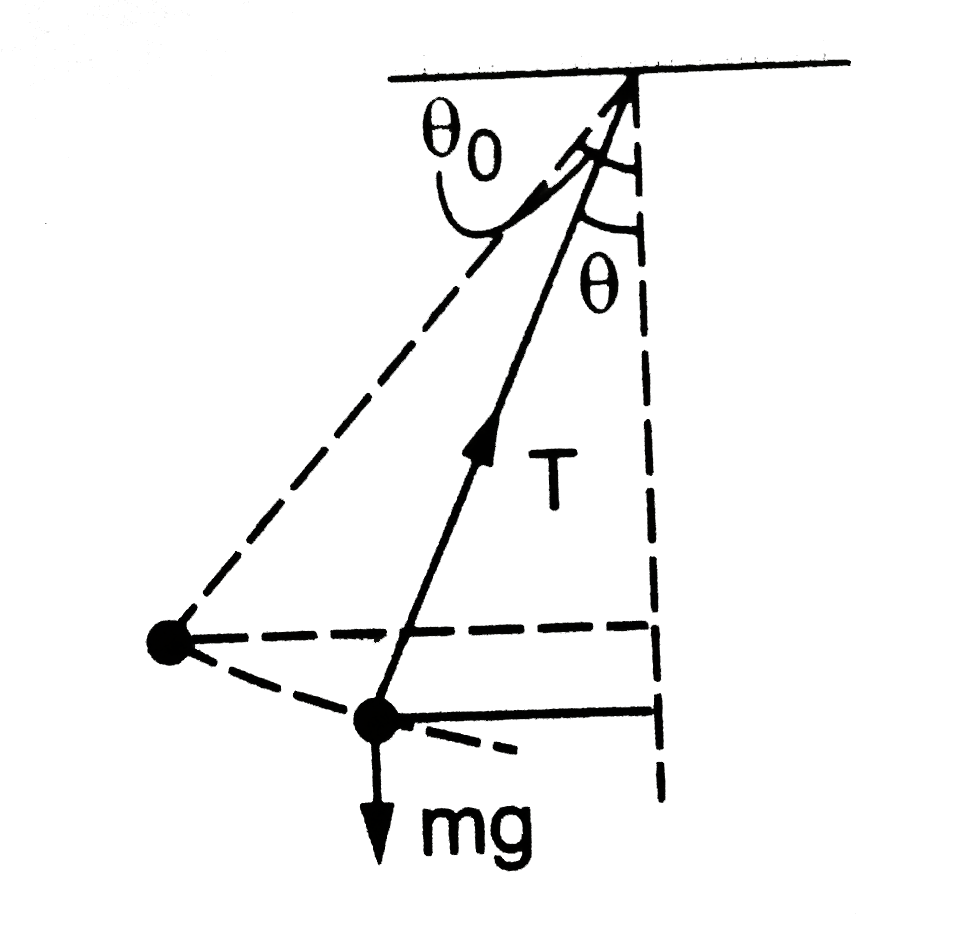
As the bob moves in a circular path, the force towards the centre shoudl the equal to mv2l. Thus,
T−mgcosθ=mv2l
<br>usingi<br>ort T-mgcostheta=2mg(costheta-costheta_0)<br>orT=3mgcostheta-2mgcostheta)<br>Nowcosthetaismaxiμmatθ=0anddecreasesas|theta| increases (for |theta|lt90^@).<br>Thusthetensionismaxiμmwhentheta=0, i.e.atthemeanpositionandisminiμmwhentheta=+-theta_0 i.e., at extreme positions
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View Solution
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
AT=mgcosθ for all value of θBT=mgcosθ for only θ=ϕCT=mg,forθ=cos−1[13(2cosϕ+1)]DT will be larger for smaller values of θTension in the string is minimum when the pendulum is at
Amean positionBextreme positionCmid way between mean and extreme positionDany position
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionA simple pendulum oscillates with an anglular amplitude of θ. If the maximum tension in the string is 3 times the minimum tension, then the value of cosθ is
View SolutionA simple pendulum with a bob of mass 'm' swings with angular amplitude of 60∘. When its angular displacement is 30∘, the tension in the strings would be
View Solutiona simple pendulum with a bob of mass m savings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the strings is-
View Solution