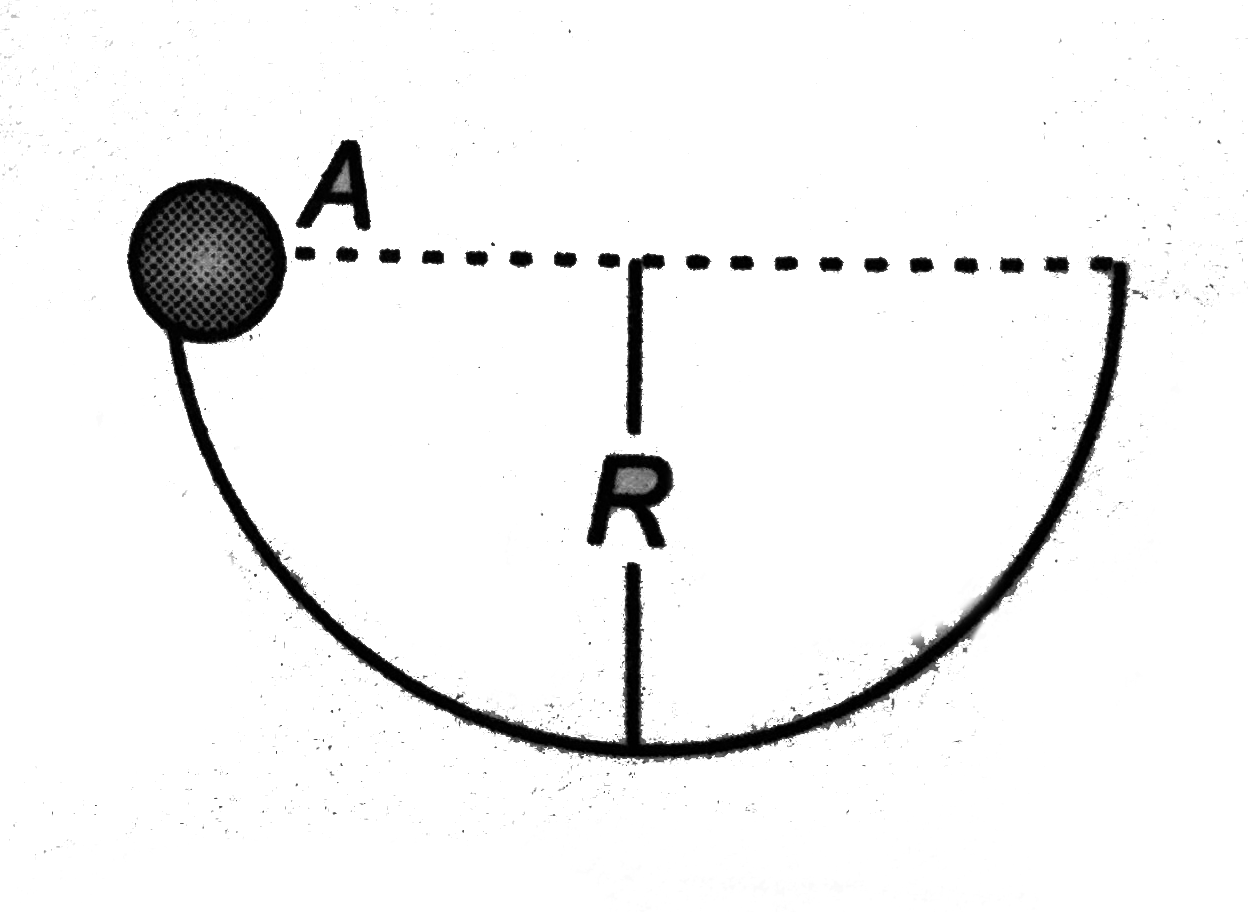
A small solid cylinder of radius r is released coaxially from point A inside the fixed large cylindrical bawl of radius R as shown in figure. If the friction between the small and the large cylinder is sufficient enough to prevent any slipping then find.
(a). What fractions of the total energy are translational and rotational when the small cylinder reaches the bottom of the larger one?
(b). The normal force exerted by the small cylinder on the larger one when it is at the bottom.
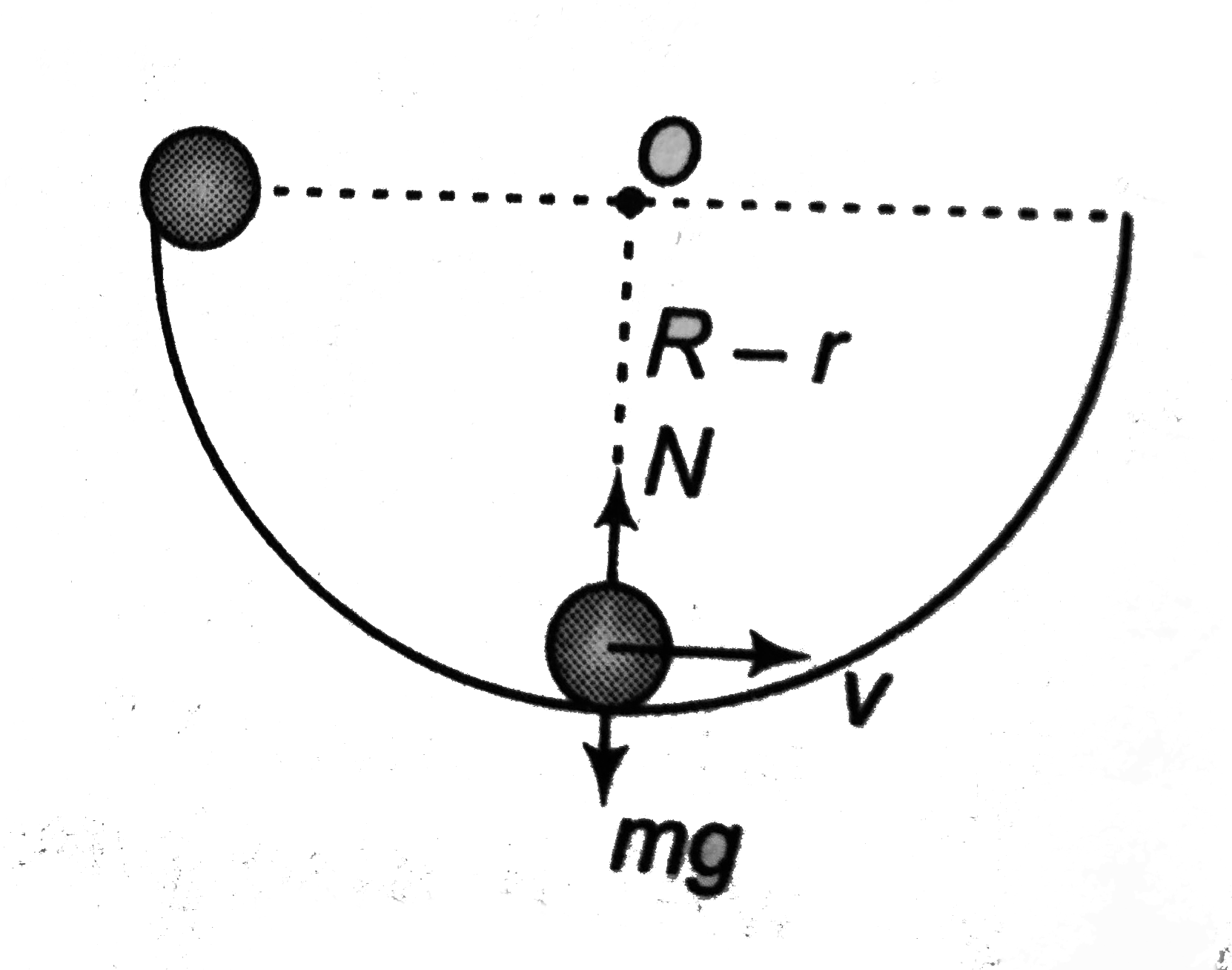
(a). Ktrans=12mv2
Krot=12Iω2=12(12mr2)(vr)2=14mv2
K=Ktrans+Krot=34mv2
∴KtransK=23⇒KrotK=13
(b). From conservation of energy
mg(R−r)=34mv2
∴mv2R−r=43mg
Now, N−mg=mv2R−r= centripetal for =43mg
∴N=73mg
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
When a solid cylinder rolls without slipping the ratio of kinetic energy of translation to its total kinetic energy is
View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View Solution
Knowledge Check
A small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
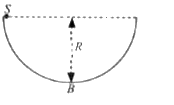 AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2
AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2A solid cylinder of radius 0.35 m is released from rest from a height of 1.8 m and rolls down the incline as shown in the figure. What is the angular speed of the cylinder when it reaches the horizontal surface?
 A8.2 rad/sB34 rad/sC14 rad/sD67 rad/s
A8.2 rad/sB34 rad/sC14 rad/sD67 rad/s
A solid cylinder of mass M is attached to the spring by means of a frintionless pivot. The cylinder is placed on floor. Find the time period of small oscillation of the system, if the floor is sufficiently rought to prevent any slipping of cylinder. Assume stiffness of spring to be K.A2π√7M5KB2π√5M3KC2π√3M2KD2π√MK
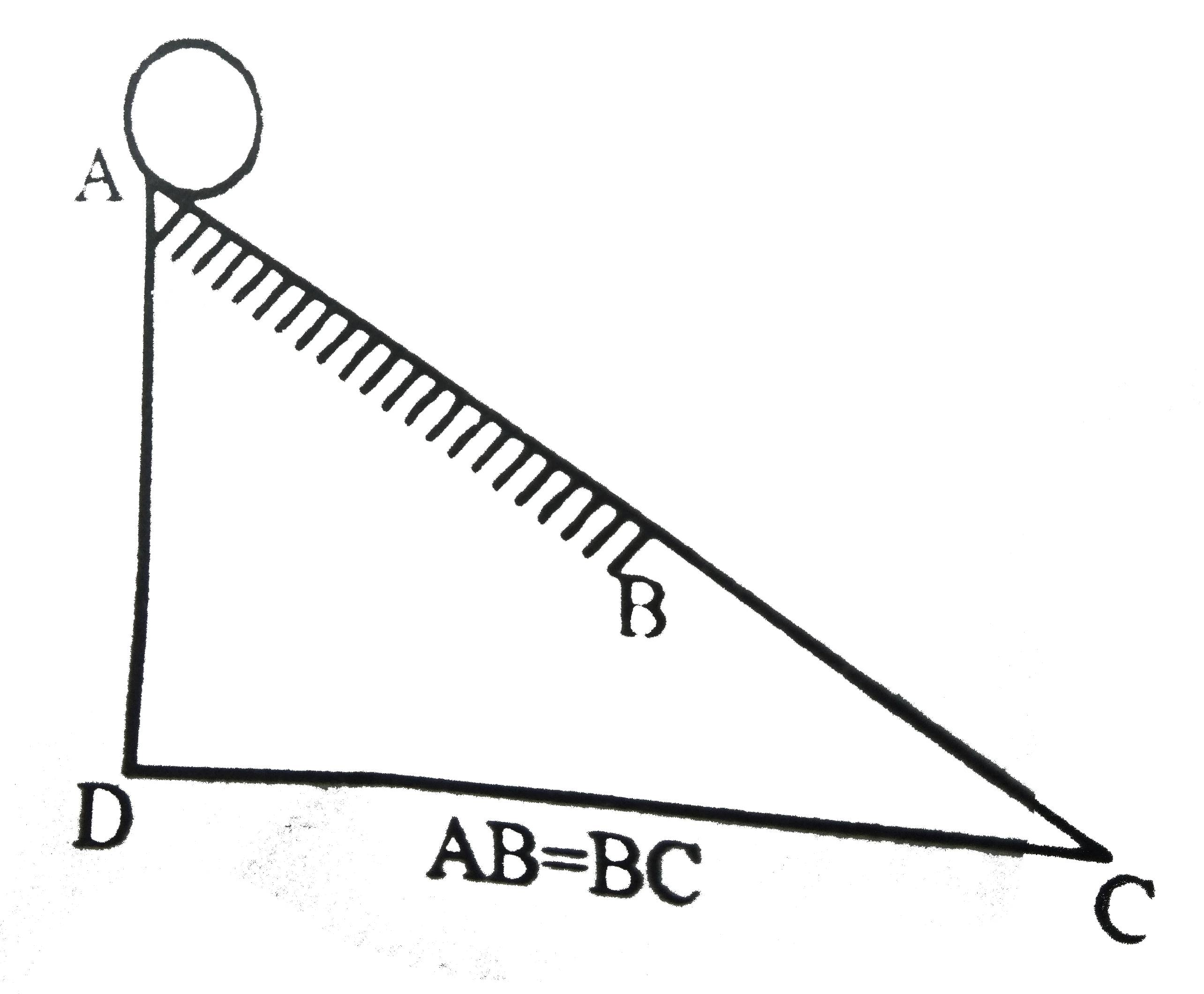
Portion AB of the wedge shown in figure is rough and BC is smooth. A solid cylinder rolld without slipping from A to B. Find the ratio of translational kinetic energy to rotationa linetic energy, when the cylinder reaches point C.
 .
.
View SolutionIn the figure shown, the light thread is tightly wrapped on the cylinder and masses of plank and cylinder are same each equal to m. An external agent begins to pull the plank to the right with a constant force F. The friction between the plank and the cylinder is large enough to prevent slipping. Assume that the length of the plank is quite large and the cylinder does not fall off it for the time duration concerned.
(a) Find the acceleration of the cylinder. (Hint : don’t write any equations)
(b) Find the kinetic energy of the system after time t.
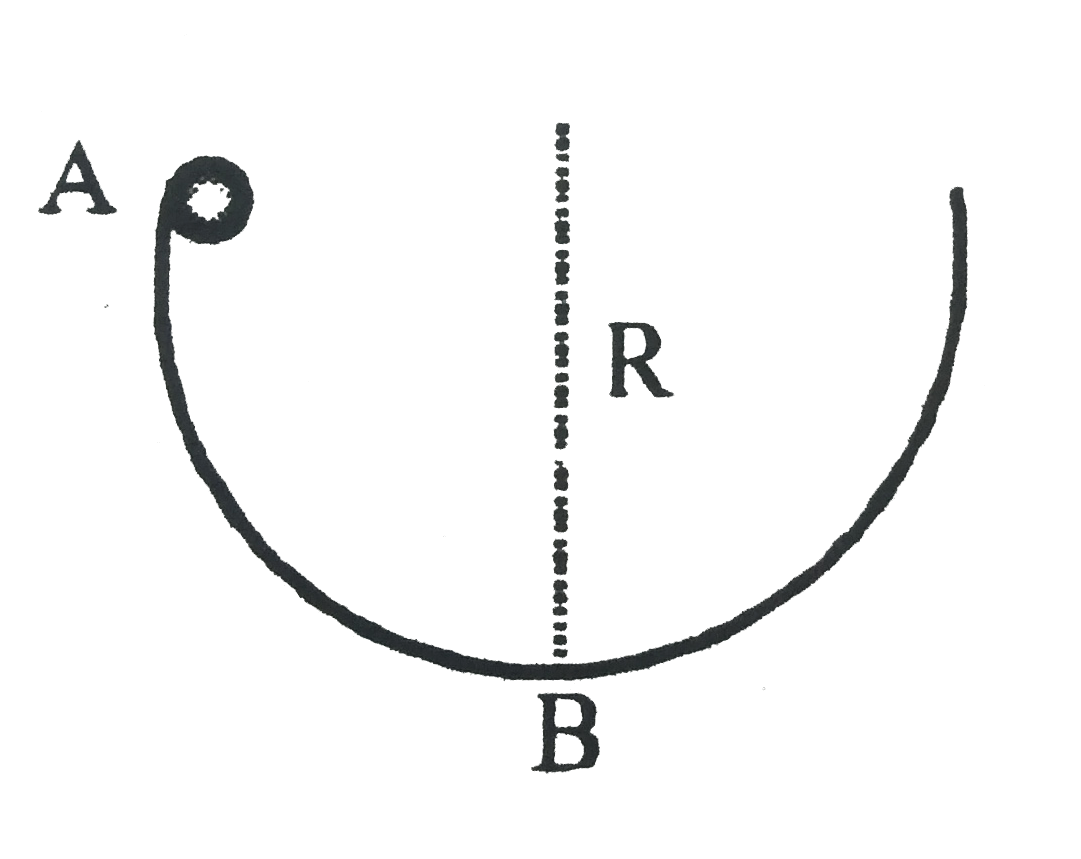
View SolutionA small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
 .
.
View SolutionPortion AB of the wedge shown in figure is rough and BC is smooth. A solid cylinder rolld without slipping from A to B. Find the ratio of translational kinetic energy to rotationa linetic energy, when the cylinder reaches point C.
 .
.
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View Solution
