A spherical conductor of radius is charged to a potential of . It is now placed inside another hollow spherical conductor of radius . Calculate the potential to which the bigger sphere would be raised
20 V
60 V
80 V
40 V
The correct Answer is:D
To solve the problem, we need to calculate the potential to which the bigger spherical conductor will be raised when the smaller charged spherical conductor is placed inside it.
1. Identify the Given Values:
- Radius of the inner sphere (R1) = 2 m
- Potential of the inner sphere (V1) = 120 V
- Radius of the outer sphere (R2) = 6 m
2. Calculate the Charge on the Inner Sphere:
The potential (V) of a charged sphere is given by the formula:
V=k⋅QR
where k is Coulomb's constant, Q is the charge, and R is the radius of the sphere.
Rearranging the formula to find the charge Q:
Q=V⋅Rk
Substituting the values for the inner sphere:
Q1=V1⋅R1=120V⋅2m=240C
3. Calculate the Potential of the Outer Sphere:
When the inner sphere is placed inside the outer sphere, it will influence the potential of the outer sphere. The potential (V2) at the surface of the outer sphere due to the charge Q1 on the inner sphere is given by:
V2=k⋅Q1R2
Substituting the values:
V2=k⋅240C6m
4. Calculate the Potential Increase:
Since k is a constant, we can simplify the equation. The potential increase at the outer sphere due to the inner sphere is:
V2=2406=40V
5. Final Potential of the Outer Sphere:
The potential of the outer sphere will now be raised by this amount. Therefore, the total potential of the outer sphere becomes:
Vtotal=Vinitial+V2
Since the outer sphere was initially uncharged, its initial potential can be considered as 0 V. Thus:
Vtotal=0+40V=40V
Conclusion:
The potential to which the bigger sphere would be raised is 40 V.
- Radius of the inner sphere (R1) = 2 m
- Potential of the inner sphere (V1) = 120 V
- Radius of the outer sphere (R2) = 6 m
The potential (V) of a charged sphere is given by the formula:
V=k⋅QR
where k is Coulomb's constant, Q is the charge, and R is the radius of the sphere.
Q=V⋅Rk
Substituting the values for the inner sphere:
Q1=V1⋅R1=120V⋅2m=240C
When the inner sphere is placed inside the outer sphere, it will influence the potential of the outer sphere. The potential (V2) at the surface of the outer sphere due to the charge Q1 on the inner sphere is given by:
V2=k⋅Q1R2
Substituting the values:
V2=k⋅240C6m
Since k is a constant, we can simplify the equation. The potential increase at the outer sphere due to the inner sphere is:
V2=2406=40V
The potential of the outer sphere will now be raised by this amount. Therefore, the total potential of the outer sphere becomes:
Vtotal=Vinitial+V2
Since the outer sphere was initially uncharged, its initial potential can be considered as 0 V. Thus:
Vtotal=0+40V=40V
The potential to which the bigger sphere would be raised is 40 V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A spherical conductor of radius 2 m is charged to a potential of 120 V. It is now placed inside another hollow spherical conductor of radius 6 m. calculate the potential of bigger sphere, if the smaller sphere is made to touch the bigger sphere
View Solution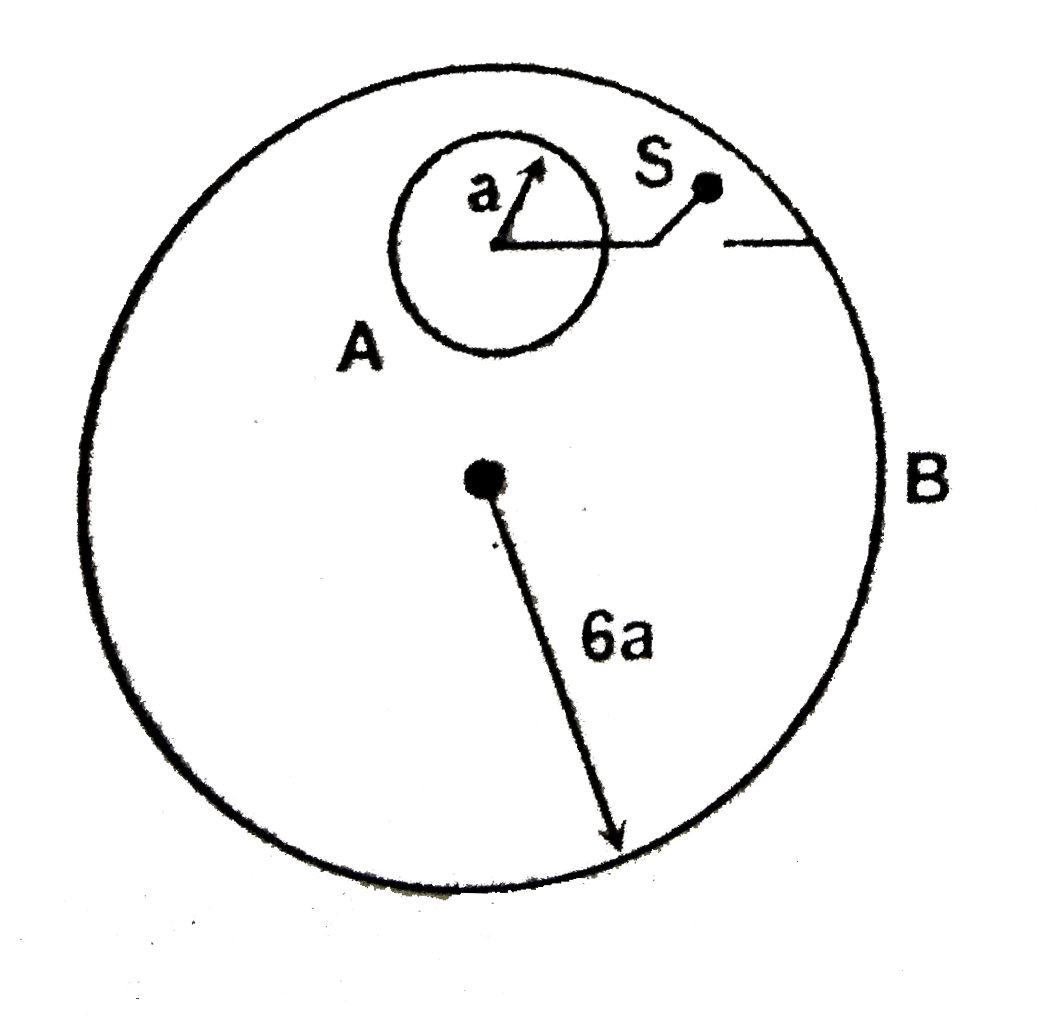
A small spherical conductor 'A' of radias 'a' is initially charged to a potential 'V' and then placed inside an uncharged spherical conducting shell 'B' of radius 6a as shown. The potential of the spherical conductor 'A' after closing the switch S is
View Solution
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
Capacitance (in F) of a spherical conductor with radius 1m is
View SolutionA hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View SolutionA hollow spherical conductor of radius r potential of 100 V at its outer surface. The potential inside the hollow at a distance ofr2 from its centre is
View SolutionA spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.
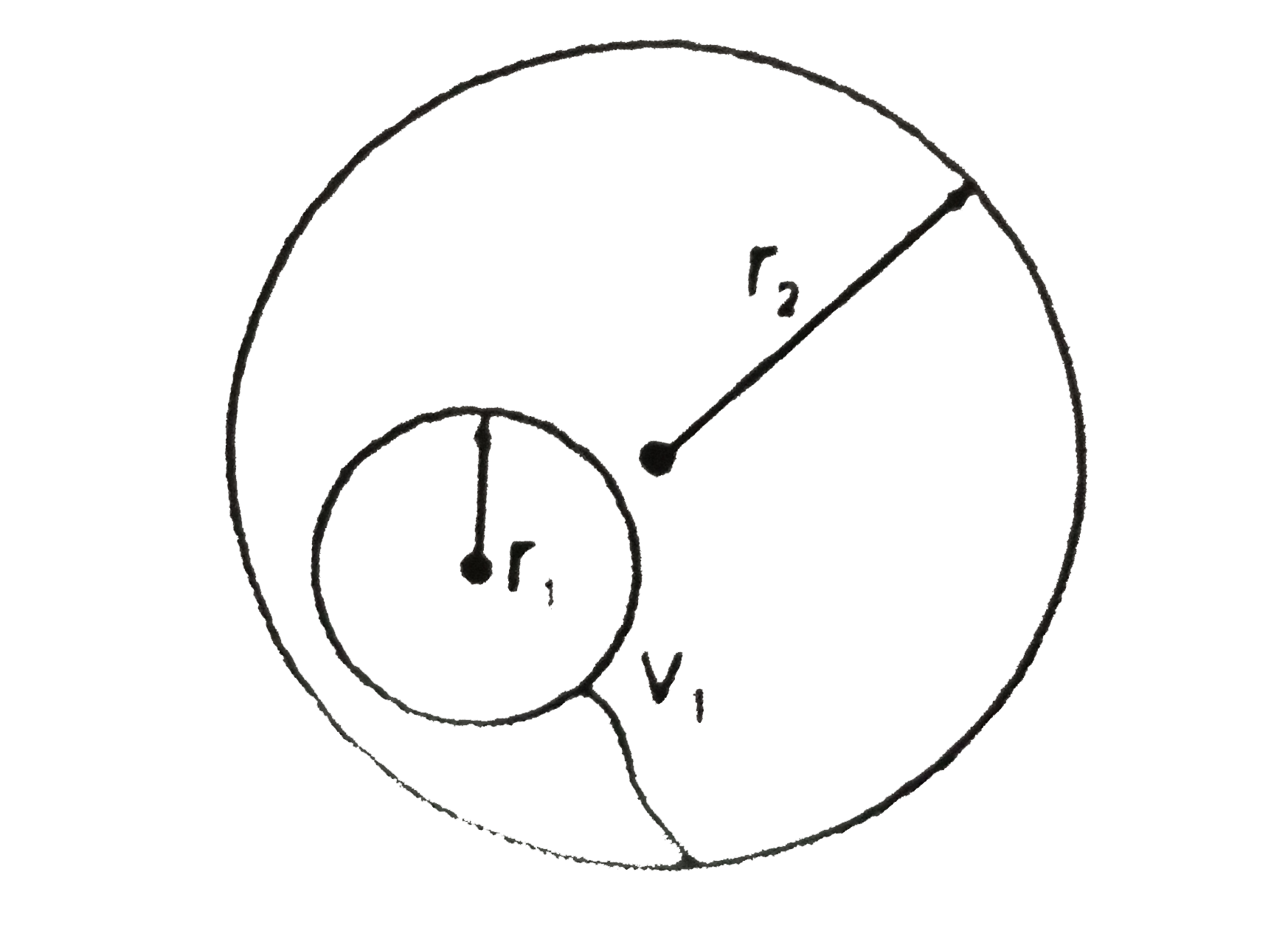
View SolutionA metal sphere of radius r1 charges to a potential V1 is then placed in a thin-walled uncharged conducting spherical shell of radius r2. Determine the potential acquired by the spherical shell after it has been connected for a short time to the sphere by a conductor.
View SolutionA hollow spherical conductor of radius 1m has a charge of 250μC then electric intensity at a point distance of 0.5m from the centre of the spherical conductor is
View SolutionA number of spherical conductors of different radius have same potential. Then the surface charge density on them.
View Solution
