A spring stores 5J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
0.16kg
1.6kg
16kg
0.016kg
The correct Answer is:C
To solve the problem, we need to find the mass of the block attached to the spring, given the energy stored in the spring and the frequency of oscillation. Here’s a step-by-step solution:
Step 1: Understand the potential energy stored in the spring
The potential energy (PE) stored in a spring when it is stretched or compressed is given by the formula:
PE=12kx2
where:
- k is the spring constant,
- x is the displacement from the equilibrium position.
Step 2: Convert displacement to meters
The displacement given is 25 cm. We need to convert this to meters:
x=25cm=0.25m
Step 3: Set up the equation for potential energy
We know the potential energy stored in the spring is 5 J. Substituting the values into the potential energy formula:
5=12k(0.25)2
Step 4: Solve for spring constant k
Rearranging the equation to solve for k:
5=12k(0.0625)
5=0.03125k
k=50.03125=160N/m
Step 5: Use the formula for the period of oscillation
The period T of oscillation for a mass-spring system is given by:
T=2π√mk
We also know that frequency f is the reciprocal of the period:
f=1T
Given that the frequency is 5 oscillations per second:
T=15s
Step 6: Substitute T into the period formula
Substituting T into the period formula:
15=2π√m160
Step 7: Square both sides to eliminate the square root
Squaring both sides gives:
(15)2=(2π)2m160
125=4π2m160
Step 8: Solve for mass m
Rearranging the equation to solve for m:
m=16025⋅4π2
Calculating 4π2:
4π2≈39.478
Thus:
m=16025⋅39.478
m≈160986.95≈0.162kg
Conclusion
The mass of the block is approximately:
m≈0.16kg
---
The potential energy (PE) stored in a spring when it is stretched or compressed is given by the formula:
PE=12kx2
where:
- k is the spring constant,
- x is the displacement from the equilibrium position.
The displacement given is 25 cm. We need to convert this to meters:
x=25cm=0.25m
We know the potential energy stored in the spring is 5 J. Substituting the values into the potential energy formula:
5=12k(0.25)2
Rearranging the equation to solve for k:
5=12k(0.0625)
5=0.03125k
k=50.03125=160N/m
The period T of oscillation for a mass-spring system is given by:
T=2π√mk
We also know that frequency f is the reciprocal of the period:
f=1T
Given that the frequency is 5 oscillations per second:
T=15s
Substituting T into the period formula:
15=2π√m160
Squaring both sides gives:
(15)2=(2π)2m160
125=4π2m160
Rearranging the equation to solve for m:
m=16025⋅4π2
Calculating 4π2:
4π2≈39.478
Thus:
m=16025⋅39.478
m≈160986.95≈0.162kg
The mass of the block is approximately:
m≈0.16kg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMAChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 2 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMAChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Exercises
Explore 32 Videos
Similar Questions
A vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View SolutionA vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View Solution
Knowledge Check
A spring of spring constant k stores 5 J of energy when stretched by 25 cm. It is kept vertical with one end fixed. A mass m is attached to the other end. It maskes 5 Oscillation per second. Then
Am=0.16kgBm=0.32kgCk=160NmDk=320NmTwo springs fixed at one end are stretched by 4 cm and 12 cm, respectively, when masses of 0.5 kg and 1 kg are suspended at their lower ends. They are displaced slightly from their mean positions and released. What is the ratio of their periods of oscillation ?
A1:√2B1:2C1:√3D2:5A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthA(a) 5ms−1B(b) 3ms−1C(c) 6ms−1D(d) None of these
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA spring of force constant 200Nm−1 has a block of mass 10 kg hanging at its one end and the other end of the spring is attached to the celling of an elevator. The elevator is rising upwards with an acceleration of g4 and the block is in equilibrium with respect to the elevator . when the acceleration of the elevator suddenly ceases , the block starts oscillating . What is the amplitude (in m) of these oscillations ?
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
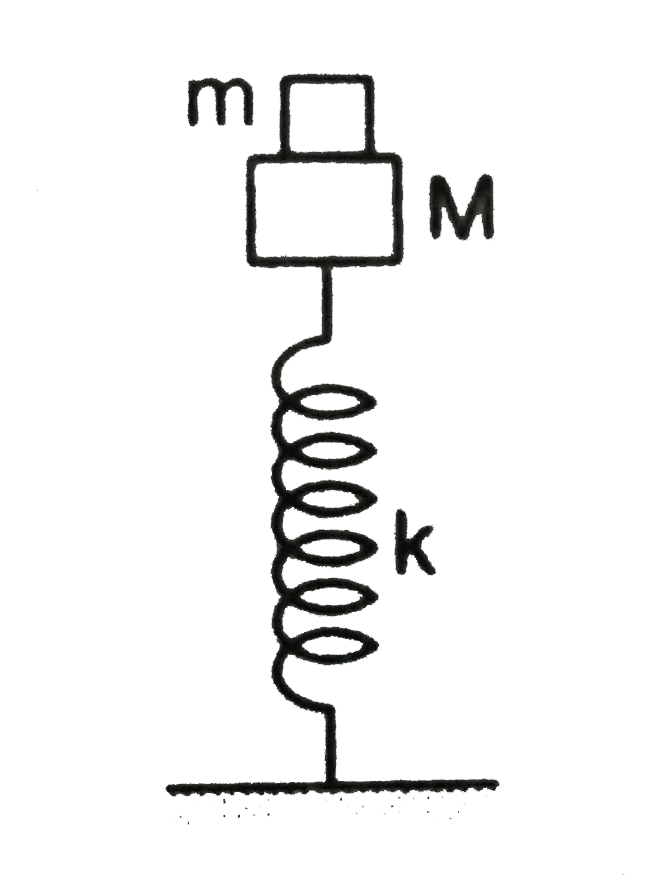
View Solution