A tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the center of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the center of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results.
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (a): Magnetic Field at the Center of the Solenoid
1. Understanding the Setup:
- We have a tightly wound solenoid of radius a and length l with n turns per unit length. It carries a current i.
- We consider a small section of the solenoid of length dx at a distance x from one end. This section contains ndx turns.
2. Current in the Small Section:
- The current in the small section can be approximated as I=ndx.
3. Magnetic Field Due to a Circular Current Loop:
- The magnetic field dB at the center of a circular current loop of radius a carrying current I is given by:
dB=μ0I2a
- For our case, substituting I=nidx:
dB=μ0(nidx)2a
4. Integrating to Find Total Magnetic Field:
- We need to integrate dB from x=0 to x=l:
B=∫l0dB=∫l0μ0(nidx)2a
- This simplifies to:
B=μ0ni2a∫l0dx=μ0ni2a⋅l
- Thus, the magnetic field at the center of the solenoid is:
B=μ0nil2a
Part (b): Analyzing the Limits
1. Case 1: l≫a:
- If the length l is much greater than the radius a, we can neglect a in comparison to l:
B \approx \frac{\mu_0 n i l}{2a} \quad \text{(as a becomes negligible)}
- This indicates that the magnetic field is primarily determined by the length of the solenoid and the current density.
2. Case 2: a≫l:
- If the radius a is much greater than the length l, we can neglect l in comparison to a:
B \approx \mu_0 n i \quad \text{(as l becomes negligible)}
- This shows that the magnetic field is uniform and primarily determined by the turns per unit length and the current.
Summary of Results:
- The magnetic field at the center of the solenoid is given by:
B=μ0nil2a
- In the limit where l≫a, the field approaches:
B≈μ0ni
- In the limit where a≫l, the field approaches:
B≈μ0nil2a
- We have a tightly wound solenoid of radius a and length l with n turns per unit length. It carries a current i.
- We consider a small section of the solenoid of length dx at a distance x from one end. This section contains ndx turns.
- The current in the small section can be approximated as I=ndx.
- The magnetic field dB at the center of a circular current loop of radius a carrying current I is given by:
dB=μ0I2a
- For our case, substituting I=nidx:
dB=μ0(nidx)2a
- We need to integrate dB from x=0 to x=l:
B=∫l0dB=∫l0μ0(nidx)2a
- This simplifies to:
B=μ0ni2a∫l0dx=μ0ni2a⋅l
- Thus, the magnetic field at the center of the solenoid is:
B=μ0nil2a
- If the length l is much greater than the radius a, we can neglect a in comparison to l:
B \approx \frac{\mu_0 n i l}{2a} \quad \text{(as a becomes negligible)}
- This indicates that the magnetic field is primarily determined by the length of the solenoid and the current density.
- If the radius a is much greater than the length l, we can neglect l in comparison to a:
B \approx \mu_0 n i \quad \text{(as l becomes negligible)}
- This shows that the magnetic field is uniform and primarily determined by the turns per unit length and the current.
- The magnetic field at the center of the solenoid is given by:
B=μ0nil2a
- In the limit where l≫a, the field approaches:
B≈μ0ni
- In the limit where a≫l, the field approaches:
B≈μ0nil2a
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.
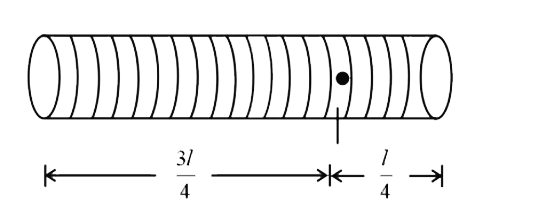
View SolutionA tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.

View Solution
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionA solenoid 50 cm long has 4 layers of windings of 350 turns each. If the current carried is 6A. Find the magnetic field at the centre of the solenoid
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionA long solenoid of 50 cm length having 100 turns carries a current of 2.5A. The magnetic field at centre of solenoid is:
View SolutionA solenoid of 2m long & 3cm diameter has 5 layers of winding of 500 turns per metre length in each layer & carries a current of 5A. Find intensity of magnetic field at the centre of the solenoid.
View Solution