A time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)

current versus time graph is a parabola
energy stored in magnetic field at t = 2 s is 4 J
potential energy at time t = 1 s in magnetic field is increasing at a rate of 1Js−1
energy stored in magnetic field is zero all the time.
The correct Answer is:A, B, C
(a, b, c) We have, V = 2t
∴ V=L.didt=2tor2.didt=2tordidt=t
or (di)=t(dt)
On integrating, we get i=t22
i.e., i-t graph is a parabola.
At t = 2 s, i= 2 A
∴ Potential energy, U=12Li2=12×2×4=4J
dUdt=Li(didt)=(2)(r22)(t)=t3
At t = 1
Potential energy, dUdt=1Js−1
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t = 0, current is zero.
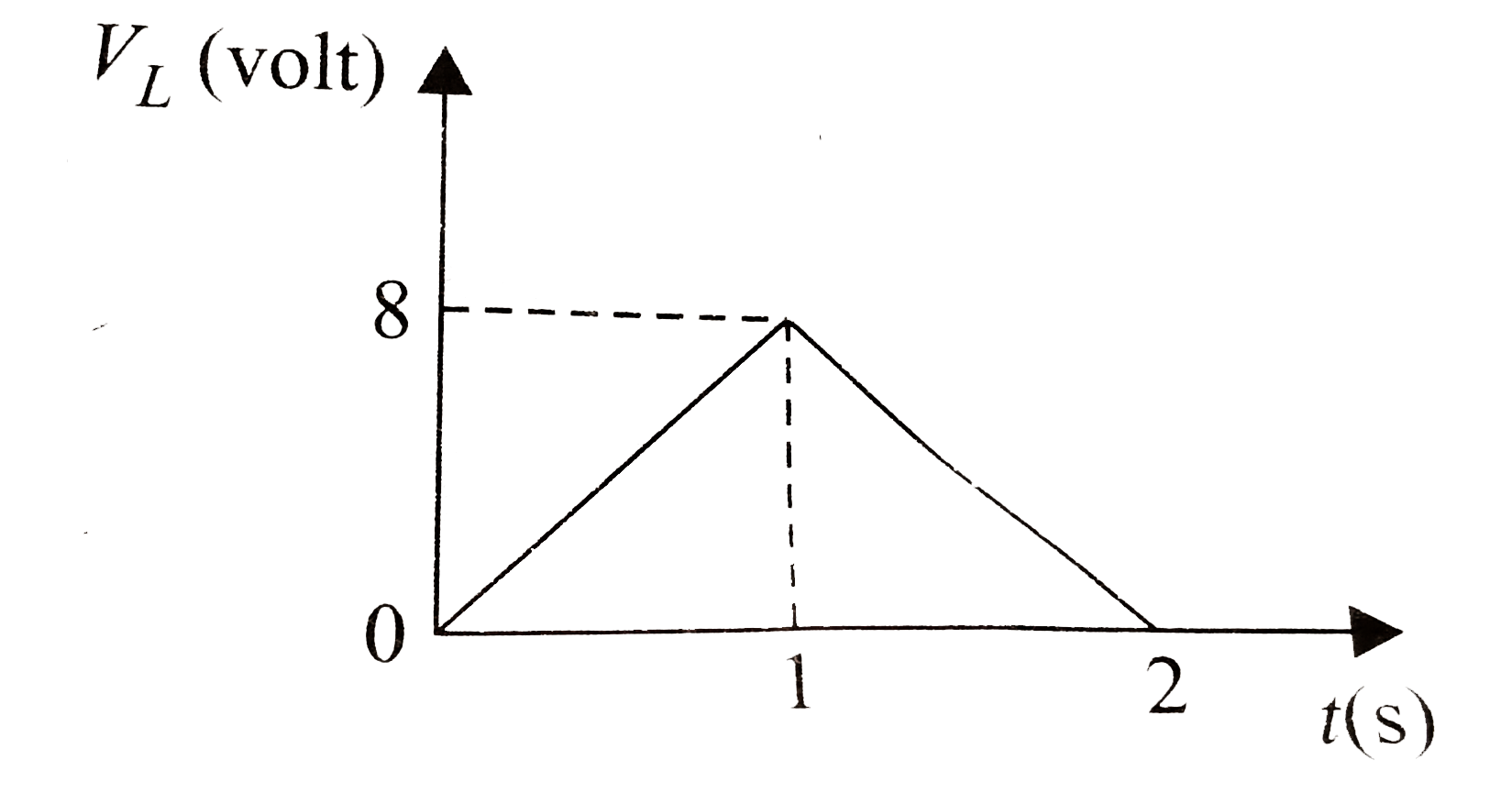
Current at t = 1 s isView SolutionA sinusoidal voltage Vsin(at) is applied across a series combination of resistance R and inductor L. The amplitude of the current in the circuit is
View SolutionThe potential difference across a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current t=2 second is
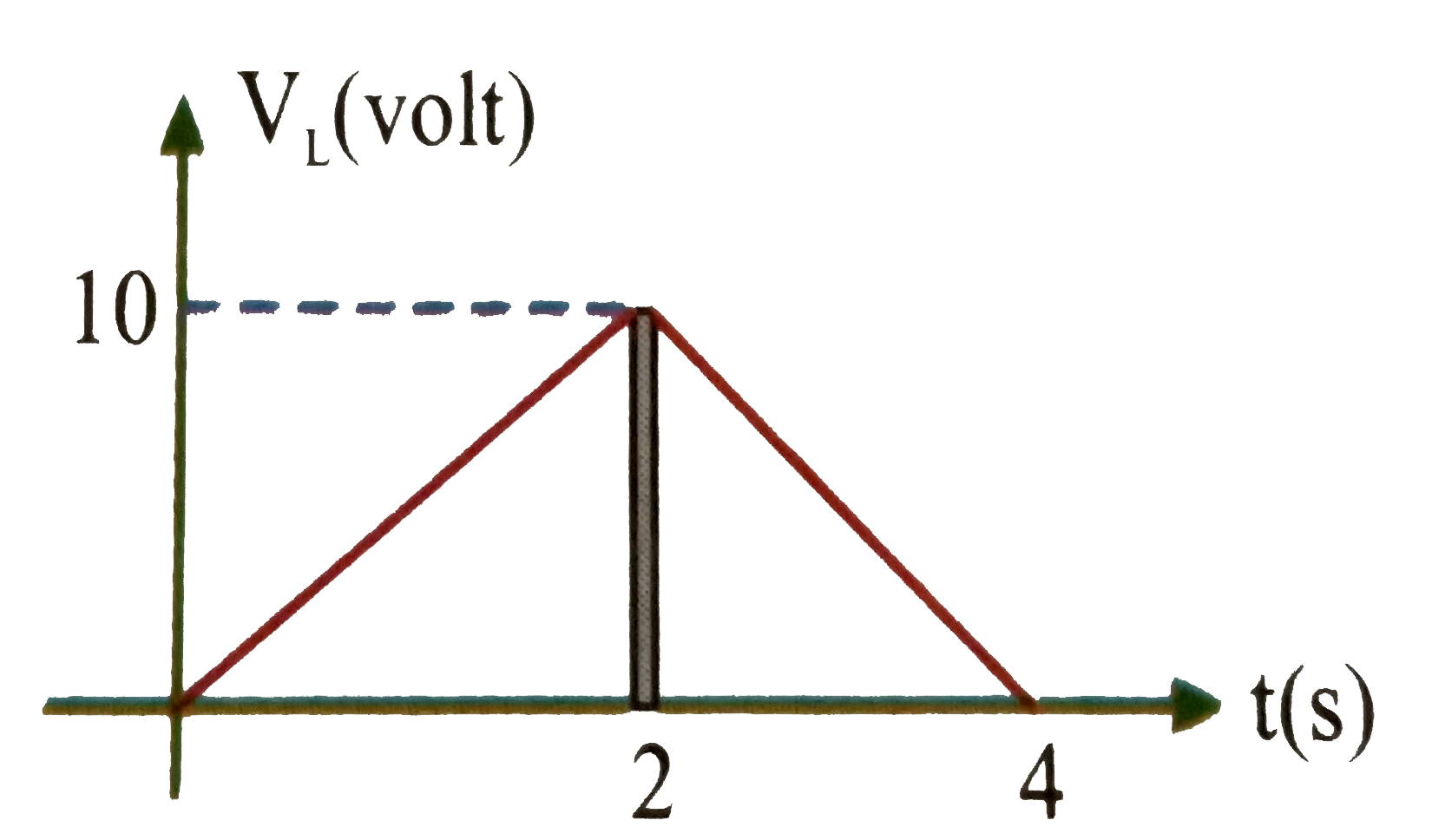 View Solution
View SolutionAn alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum isView SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum isView SolutionIn the circuit shown, a time varying voltage V=2000t volt is applied where t is in second. At time t5ms, determine the Current through the resistor R=4Ω and through the capacitor C300μF
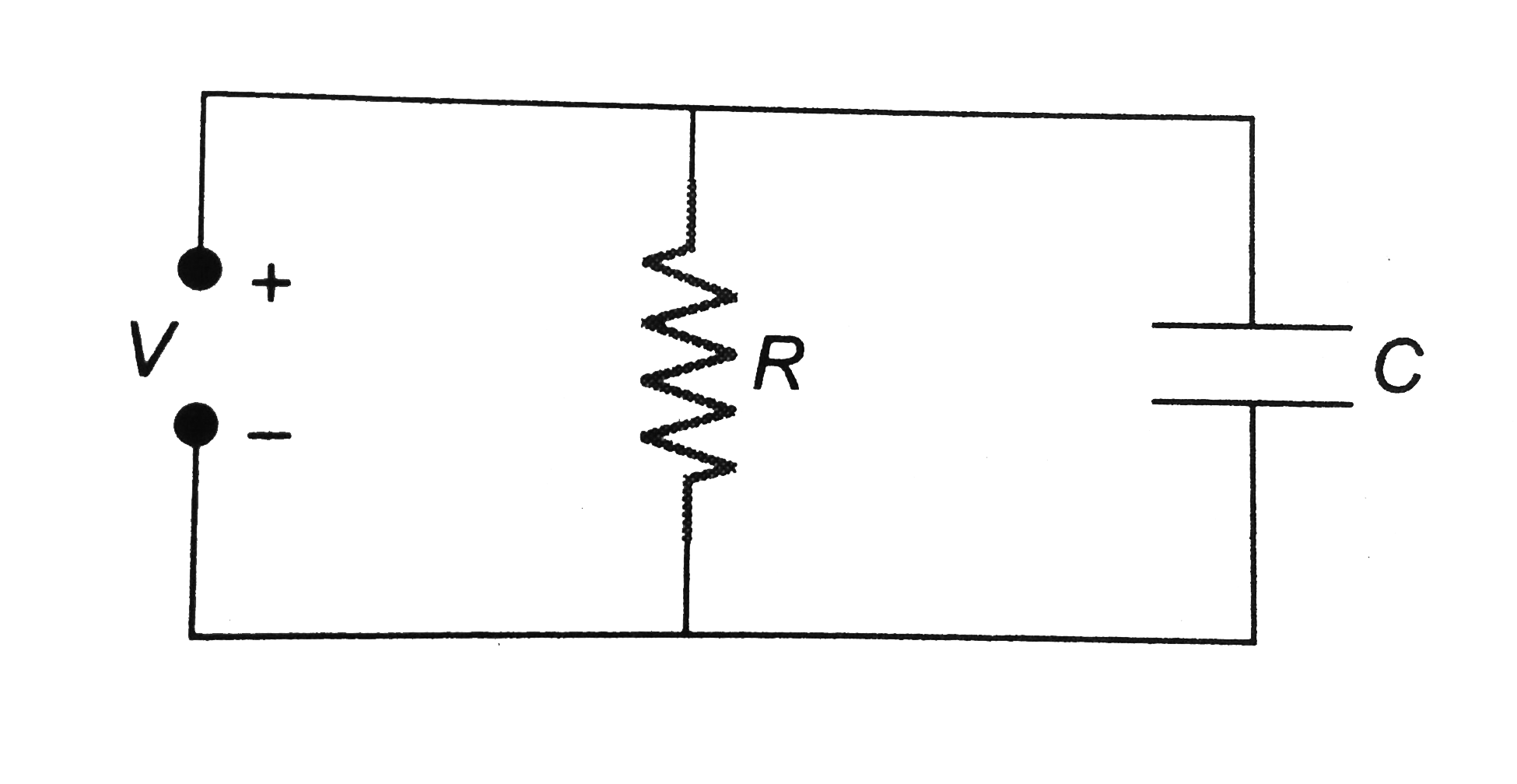 View Solution
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
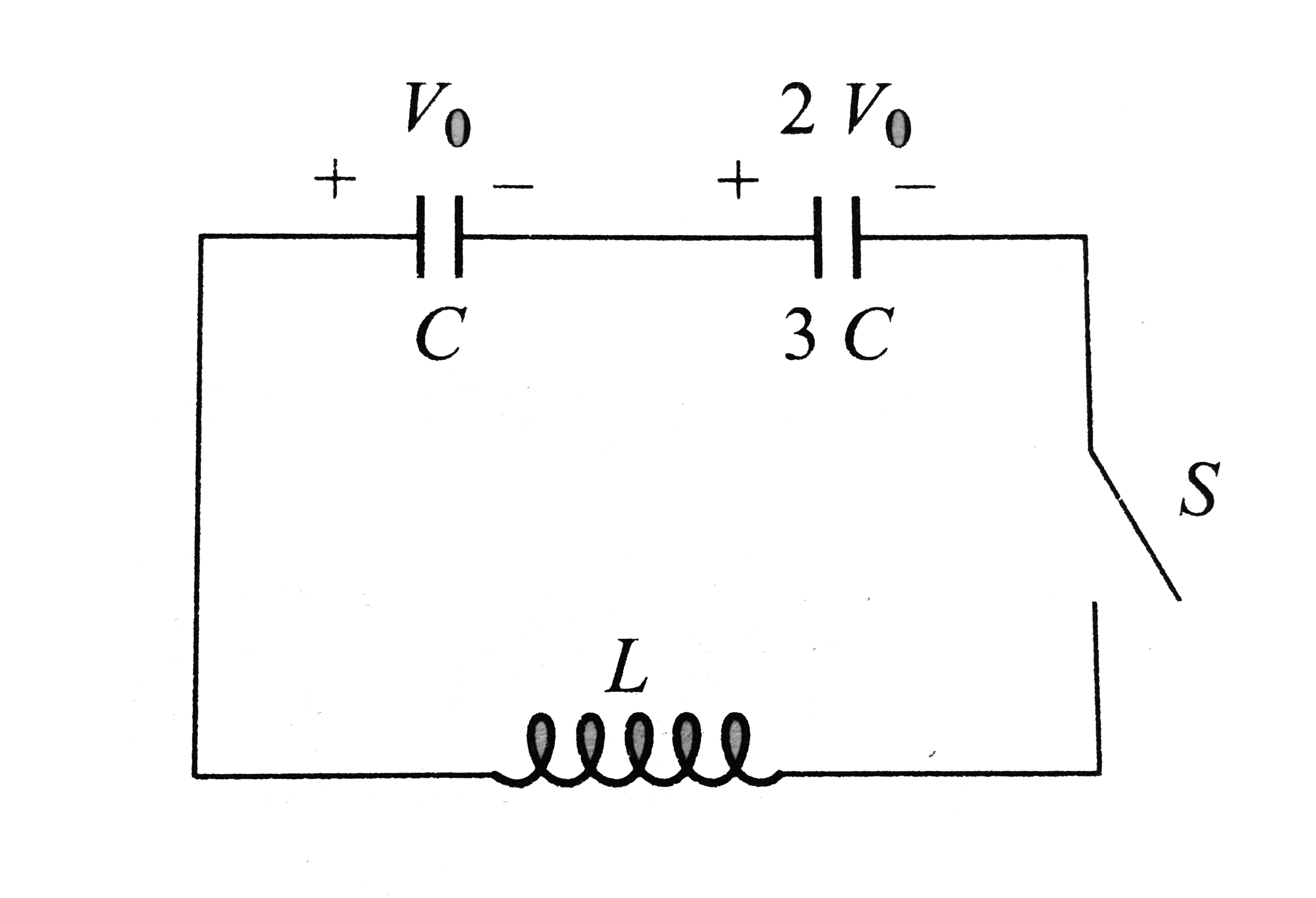
The maximum current in the inductor isView SolutionThe potential difference across a 10H inductor as a function of time is shown in the figure. At t=0 current is zero. Then
 View Solution
View Solution

