A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment →M
is non-zero and points in the Z-direaction by symmetry
points along the axis of the toroid (m=mϕ)
is zero, otherwise there would be a field falling as 1r3 at large distance outside the toriod
is pointing radially outwards
The correct Answer is:C
To find the magnetic moment →M of a toroid with n turns, mean radius R, cross-sectional radius a, and carrying current I, we can follow these steps:
Step 1: Understand the Geometry of the Toroid
A toroid can be visualized as a solenoid bent into a circular shape. The mean radius R is the average distance from the center of the toroid to the wire, while a is the radius of the cross-section of the toroid.
Step 2: Formula for Magnetic Moment
The magnetic moment →M for a toroid is given by the formula:
→M=n⋅I⋅A
where:
- n is the number of turns,
- I is the current flowing through the toroid,
- A is the area of the cross-section of the toroid.
Step 3: Calculate the Cross-sectional Area
The cross-sectional area A of the toroid can be calculated as:
A=πa2
where a is the radius of the cross-section.
Step 4: Substitute the Area into the Magnetic Moment Formula
Now, substituting the area A into the magnetic moment formula:
→M=n⋅I⋅(πa2)
Step 5: Analyze the Magnetic Moment
The direction of the magnetic moment →M is along the axis of the toroid. However, since the magnetic field is confined within the toroid and there is no magnetic field outside, we can conclude that the magnetic moment is effectively zero in the regions outside the toroid.
Step 6: Conclusion
Thus, the magnetic moment →M exists within the toroid but is zero in the surrounding space. Therefore, the magnetic moment is:
→M=n⋅I⋅πa2
and it is confined to the interior of the toroid.
A toroid can be visualized as a solenoid bent into a circular shape. The mean radius R is the average distance from the center of the toroid to the wire, while a is the radius of the cross-section of the toroid.
The magnetic moment →M for a toroid is given by the formula:
→M=n⋅I⋅A
where:
- n is the number of turns,
- I is the current flowing through the toroid,
- A is the area of the cross-section of the toroid.
The cross-sectional area A of the toroid can be calculated as:
A=πa2
where a is the radius of the cross-section.
Now, substituting the area A into the magnetic moment formula:
→M=n⋅I⋅(πa2)
The direction of the magnetic moment →M is along the axis of the toroid. However, since the magnetic field is confined within the toroid and there is no magnetic field outside, we can conclude that the magnetic moment is effectively zero in the regions outside the toroid.
Thus, the magnetic moment →M exists within the toroid but is zero in the surrounding space. Therefore, the magnetic moment is:
→M=n⋅I⋅πa2
and it is confined to the interior of the toroid.
Similar Questions
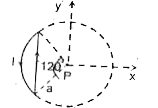
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionA toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil of radius 10cmand100 turns carries a current 1A. What is the magnetic moment of the coil?
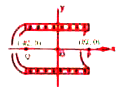
View SolutionA solenoid of length 'l' has N turns of wire closely spaced, each turn carrying a current i. If R is cross sectional radius of the solenoid, the magnetic induction at 'P'(only axial component).
View Solution
