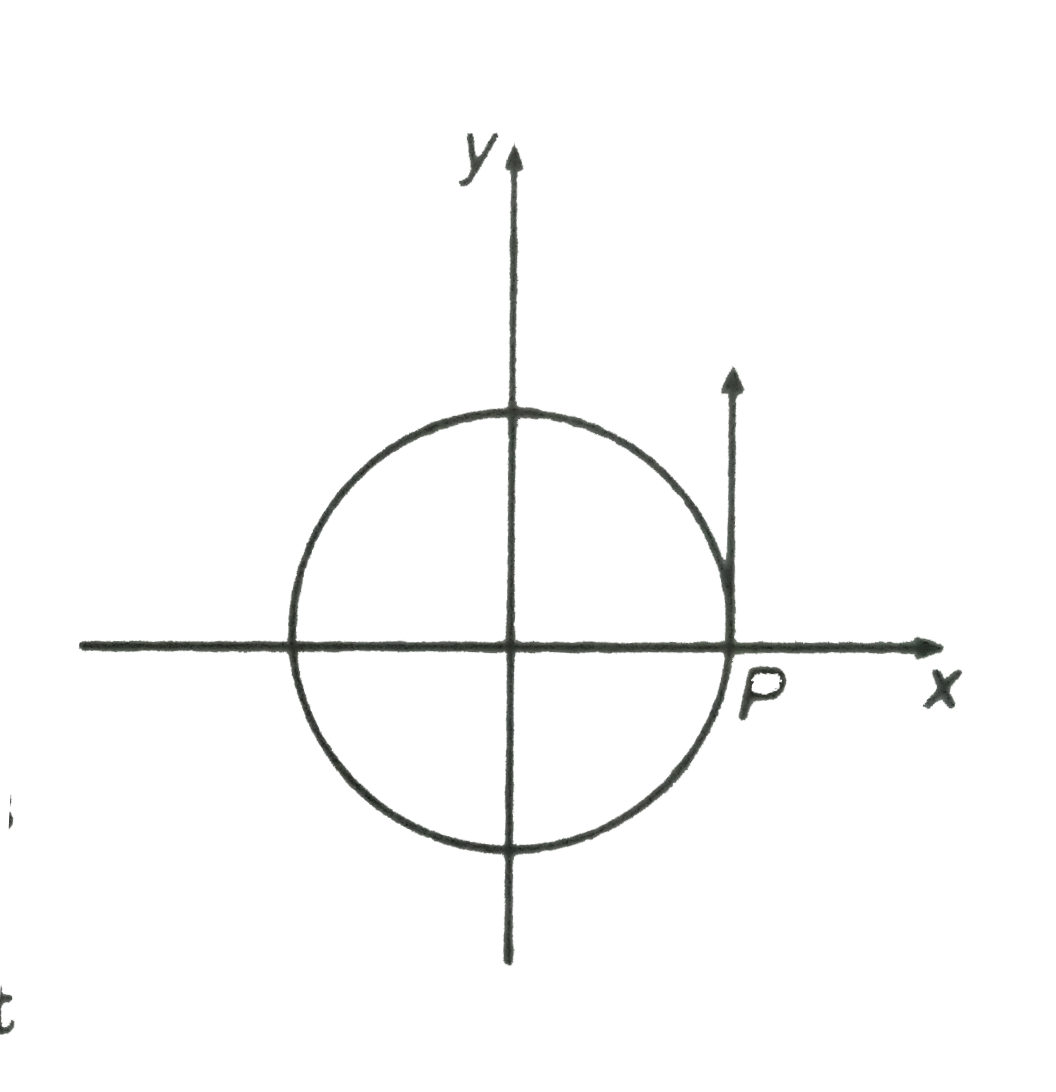
A train is moving with a constant speed of $10 m / s$ in a circle of radius $\frac{16}{π}$ m. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed $10 m / s$ relative to train towards negative x-axis at an angle of $37^{\circ}$ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g $= 10 m / s^{2}, {sin 37}^{\circ} = \frac{3}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C

At t = 0 $v_{T} = (10 ˆ j) m / s$
$v_{S T} = 10 {cos 37}^{\circ} ˆ k - 10 {sin 37}^{\circ} ˆ i = (8 ˆ k - 6 ˆ i) m / s$
$∴ V_{s} = v_{S T} + v_{T} = (- 6 ˆ i + 10 ˆ j + 8 ˆ k) m / s$
(a) At highest point vertical component $(ˆ k)$ of $v_{s}$ will become zero. Hence, velocity of particle at highest point will become $(- 6 ˆ i + 10 ˆ j) m / s$ .
(b) Time of flight, $T = \frac{2 v_{Z}}{g} = \frac{2 \times 8}{10} = 1.6 s$
$x = x_{i} + v_{x} T$
$= \frac{16}{π} - 6 \times 1.6 = - 4.5 m$
$y = (10) (1.6) = 16 m and z = 0$
Therefore , coordinates of particle where it finally
lands on the ground are $(- 4.5 m, 16 m, 0)$
At highest point, $t = \frac{T}{2} = 0.8 s$
$∴ x = \frac{16}{π} - (6) (0.8) = 0.3 m$
$y = (10) (0.8) = 8.0 m$
and $z = \frac{v_{Z}^{2}}{2 g} = \frac{{(8)}^{2}}{20} = 3.2 m$
Therefore , coordinates at highest point are,
$(0.3 m, 8.0 m, 3.2 m)$ .

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

DC PANDEY ENGLISH-PROJECTILE MOTION-Level - 2 Subjective

Home
Ask Doubt
Profile