A uniform chain of mass M and length L is held verticallyi in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length x has reached the floor.
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have a uniform chain of mass M and length L that is held vertically with its lower end just touching the floor. When released, the chain falls and any portion that strikes the floor comes to rest.
Step 2: Define the Variables
Let:
- x = length of the chain that has reached the floor.
- dm = differential mass of a small segment of the chain of length dx.
- v = velocity of the differential mass just before it strikes the floor.
Step 3: Calculate the Differential Mass
The mass per unit length of the chain is given by:
ML
Thus, the differential mass dm for a small length dx is:
dm=ML⋅dx
Step 4: Determine the Velocity Just Before Collision
Using the principle of conservation of energy, the velocity v of the chain segment just before it strikes the floor can be derived from the potential energy:
v=√2gx
where g is the acceleration due to gravity.
Step 5: Calculate the Rate of Change of Momentum
The change in momentum dp for the differential mass dm when it strikes the floor is:
dp=dm⋅v=(ML⋅dx)⋅√2gx
Step 6: Find the Force Exerted on the Floor
The force F1 exerted on the floor due to the differential mass is the rate of change of momentum:
F1=dpdt=ML⋅√2gx⋅dxdt
Since dxdt=v=√2gx, we can substitute:
F1=ML⋅√2gx⋅√2gx=ML⋅2gx
Thus:
F1=2MgxL
Step 7: Calculate the Weight of the Chain on the Floor
The weight F2 of the portion of the chain that has reached the floor is:
F2=Weight of the chain on the floor=mass of the chain on the floor⋅g=(ML⋅x)⋅g=MgxL
Step 8: Total Force Exerted on the Floor
The total force F exerted on the floor is the sum of F1 and F2:
F=F1+F2=2MgxL+MgxL=3MgxL
Final Answer
The force exerted by the chain on the floor when a length x has reached the floor is:
F=3MgxL
We have a uniform chain of mass M and length L that is held vertically with its lower end just touching the floor. When released, the chain falls and any portion that strikes the floor comes to rest.
Let:
- x = length of the chain that has reached the floor.
- dm = differential mass of a small segment of the chain of length dx.
- v = velocity of the differential mass just before it strikes the floor.
The mass per unit length of the chain is given by:
ML
Thus, the differential mass dm for a small length dx is:
dm=ML⋅dx
Using the principle of conservation of energy, the velocity v of the chain segment just before it strikes the floor can be derived from the potential energy:
v=√2gx
where g is the acceleration due to gravity.
The change in momentum dp for the differential mass dm when it strikes the floor is:
dp=dm⋅v=(ML⋅dx)⋅√2gx
The force F1 exerted on the floor due to the differential mass is the rate of change of momentum:
F1=dpdt=ML⋅√2gx⋅dxdt
Since dxdt=v=√2gx, we can substitute:
F1=ML⋅√2gx⋅√2gx=ML⋅2gx
Thus:
F1=2MgxL
The weight F2 of the portion of the chain that has reached the floor is:
F2=Weight of the chain on the floor=mass of the chain on the floor⋅g=(ML⋅x)⋅g=MgxL
The total force F exerted on the floor is the sum of F1 and F2:
F=F1+F2=2MgxL+MgxL=3MgxL
The force exerted by the chain on the floor when a length x has reached the floor is:
F=3MgxL
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
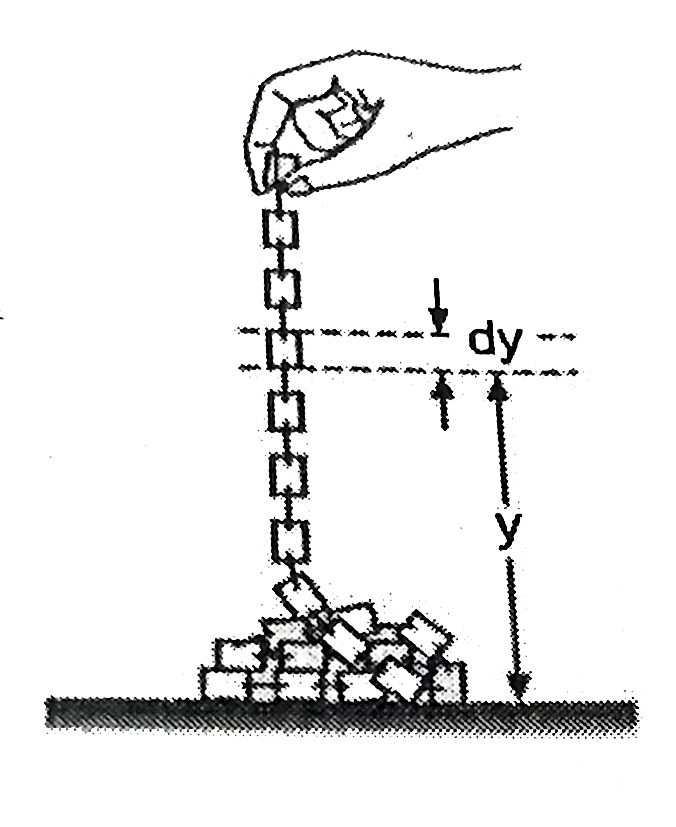
View SolutionA very flexible uniform chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest the instant it strikes the floor of the lift.Find the force exerted by the floor of the lift on the chain at the moment, when one fourth of the chain has already rested on the floor. Assume that lift is moving up with an acceleration g/2.
View Solution
Knowledge Check
A uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length x has reached the floor.
A5 NB10 NC15 ND20 NA chain of mass M and length l is held vertically such that its bottom end just touches the surface of a horizontal table. The chain is released from rest. Assume that the portion of chain on the table does not form a heap. The momentum of the portion of the chain above the table after the top end of the chain falls down by a distance l8.
A314M√glB316M√glC716M√glD914M√glA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
AMgBMg(L−y)/LCMgL/(L−y)DMgy/L
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
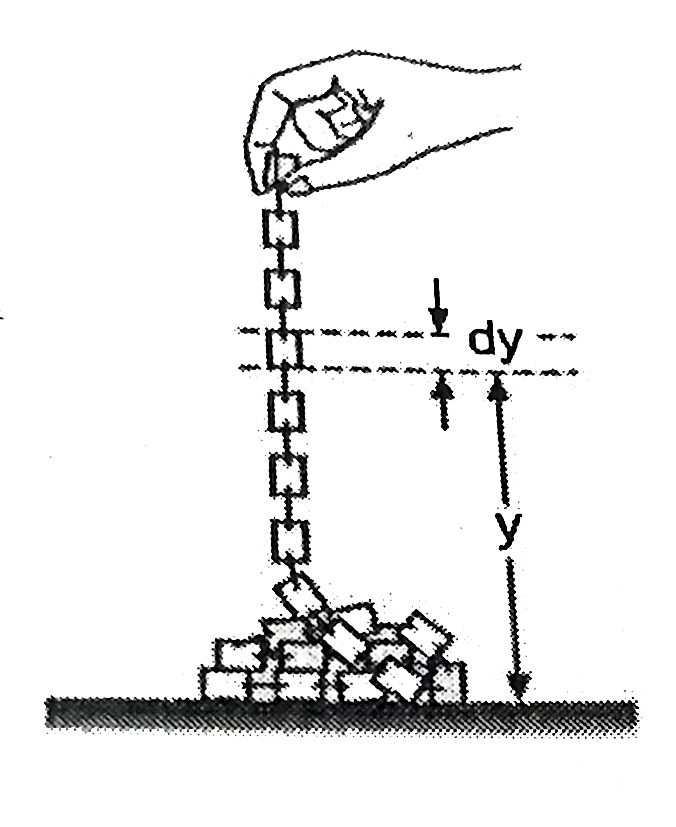
View SolutionA very flexible unifrom chain of mass M and length L is suspended vertically so that its lower end just touches the surface of a table When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table Find the force exerted by the chain on the table at the moment when x part of chain has already rested on the table .
View SolutionA rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View SolutionA very flexible chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest intantaneously find the force exerted by the floor of the lift on the chain at the moment when one fourth of the chain has already landed on the floor Assume the lift is moving with acceleration g/2
View SolutionA uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
View Solution
