A uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
14mg
2mg
12mg
23mg
The correct Answer is:D
To solve the problem of finding the minimum value of the horizontal force F required for the cube to begin to topple without sliding, we can follow these steps:
1. Understand the Setup:
- We have a uniform cube with side length A and mass m resting on a rough horizontal surface.
- A horizontal force F is applied at a height of A4 above the center of one face of the cube.
2. Identify Key Points:
- The center of the cube is at height A2 from the base.
- The point where the force F is applied is at height A4 above the center, which means it is at height 3A4 from the base.
3. Determine the Point of Rotation:
- The cube will begin to topple about the edge that is in contact with the ground. Let's denote this edge as point O.
4. Set Up the Moment Equation:
- For the cube to begin to topple, the moments about point O must balance. The moment due to the applied force F must equal the moment due to the weight of the cube mg.
- The distance from point O to the line of action of force F is A2 (the height of the cube) minus A4 (the height where the force is applied), which gives us A4.
- The moment due to the force F is F×A4.
- The moment due to the weight mg is mg×A2.
5. Write the Moment Balance Equation:
F⋅A4=mg⋅A2
6. Solve for F:
- Rearranging the equation gives:
F=mg⋅A2A4=mg⋅21=2mg
- However, we need to consider the height at which the force is applied. The correct distance for the force F is actually 3A4 from point O.
- Thus, the moment equation should be:
F⋅3A4=mg⋅A2
- Solving this gives:
F=mg⋅A23A4=mg⋅23=23mg
7. Final Result:
- The minimum value of the force F for which the cube begins to topple above an edge without sliding is:
F=23mg
- We have a uniform cube with side length A and mass m resting on a rough horizontal surface.
- A horizontal force F is applied at a height of A4 above the center of one face of the cube.
- The center of the cube is at height A2 from the base.
- The point where the force F is applied is at height A4 above the center, which means it is at height 3A4 from the base.
- The cube will begin to topple about the edge that is in contact with the ground. Let's denote this edge as point O.
- For the cube to begin to topple, the moments about point O must balance. The moment due to the applied force F must equal the moment due to the weight of the cube mg.
- The distance from point O to the line of action of force F is A2 (the height of the cube) minus A4 (the height where the force is applied), which gives us A4.
- The moment due to the force F is F×A4.
- The moment due to the weight mg is mg×A2.
F⋅A4=mg⋅A2
- Rearranging the equation gives:
F=mg⋅A2A4=mg⋅21=2mg
- However, we need to consider the height at which the force is applied. The correct distance for the force F is actually 3A4 from point O.
- Thus, the moment equation should be:
F⋅3A4=mg⋅A2
- Solving this gives:
F=mg⋅A23A4=mg⋅23=23mg
- The minimum value of the force F for which the cube begins to topple above an edge without sliding is:
F=23mg
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct86videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.View SolutionIf the friction is sufficient to prevent the block from sliding, then the minimum value of F for which the cube begins to topple about an edge is
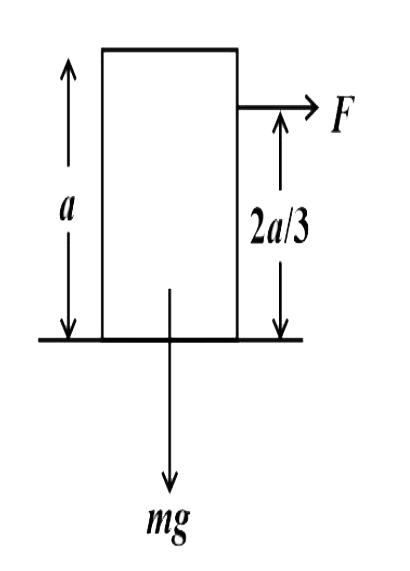 View Solution
View SolutionA uniform sphere is place on a smooth horizontal surface and as horizontal force F is appied on it at a distance h above the surface. The acceleratioin of the centre
View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is
 View Solution
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionA unifrom cube of mass m and side a is placed on a frictionless horizontal surface .A vertical force F is applied to the edge as shown in figure ,match the following (most appropriate choice )
 View Solution
View Solution

