A uniform electric field E0 is directed along positive y-driection. Find the change in electric potential energy of a positive test charge q0 when it is displaced in this field from yi=a to yf=2a along the y-axis.
To find the change in electric potential energy of a positive test charge q0 when it is displaced in a uniform electric field E0 from yi=a to yf=2a, we can follow these steps:
Step 1: Understand the relationship between electric potential energy and electric potential
The change in electric potential energy (ΔU) of a charge q0 in an electric field is given by the formula:
ΔU=q0ΔV
where ΔV is the change in electric potential.
Step 2: Calculate the change in electric potential (ΔV)
The change in electric potential (ΔV) when moving in an electric field is given by:
ΔV=Vf−Vi=−E⋅d
where E is the magnitude of the electric field and d is the displacement in the direction of the field.
Step 3: Identify the displacement
In this case, the charge is moving from yi=a to yf=2a. The displacement d is:
d=yf−yi=2a−a=a
Step 4: Determine the direction of the electric field
Since the electric field E0 is directed along the positive y-direction, the angle θ between the electric field and the displacement vector is 0∘. Therefore, we can simplify the dot product:
E⋅d=E0⋅a
Step 5: Substitute into the change in potential formula
Now substituting into the change in potential formula:
ΔV=−E0⋅a
Step 6: Calculate the change in electric potential energy
Now we can substitute ΔV into the formula for change in electric potential energy:
ΔU=q0ΔV=q0(−E0⋅a)=−q0E0a
Final Result
Thus, the change in electric potential energy when the charge is displaced from y=a to y=2a is:
ΔU=−q0E0a
---
The change in electric potential energy (ΔU) of a charge q0 in an electric field is given by the formula:
ΔU=q0ΔV
where ΔV is the change in electric potential.
The change in electric potential (ΔV) when moving in an electric field is given by:
ΔV=Vf−Vi=−E⋅d
where E is the magnitude of the electric field and d is the displacement in the direction of the field.
In this case, the charge is moving from yi=a to yf=2a. The displacement d is:
d=yf−yi=2a−a=a
Since the electric field E0 is directed along the positive y-direction, the angle θ between the electric field and the displacement vector is 0∘. Therefore, we can simplify the dot product:
E⋅d=E0⋅a
Now substituting into the change in potential formula:
ΔV=−E0⋅a
Now we can substitute ΔV into the formula for change in electric potential energy:
ΔU=q0ΔV=q0(−E0⋅a)=−q0E0a
Thus, the change in electric potential energy when the charge is displaced from y=a to y=2a is:
ΔU=−q0E0a
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Knowledge Check
A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
Aremains a constant because the electric field is uniform.Bincreases because the charge moves along the electric field.Cdecreases because the charge moves along the electric field.Ddecreases because the charge moves opposite to the electric field.
A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View SolutionThe uniform electric field is along positive y-axis positive x axis as shown in figure. The signs of potential differences VP−VQ and VB−VA respectively are
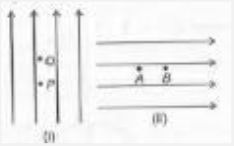
View SolutionAn electron is projected along positive z-axis, magnetic field is present along y-axis then direction of initial acceleration of the particle is
View SolutionThere exists a uniform electric field E =4 ×105Vm−3 directed along negative x-axis such that electric potential at origin is zero. A charge of - 200 μC is placed at origin and a charged of + 200 μ C is placed at a (3 m, 0) . The electrostatic potential energy of the system is
View SolutionA positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
View SolutionUniform electric field of magnitude 100Vm−1 in space is directed along the line y=3+x. Find the potential difference between points A(3,1)andB(1,3).
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View Solution

