A uniform meter stickis suspended through a small pin hole at the 10 cm mark. Find the time period of small oscillation about the point of suspension.
Let the mass of the stick be m. The moent of inertia of the stick about the axis of rotation through the point of suspension is
I=ml212+md2,
where l=1 m and d=40cm
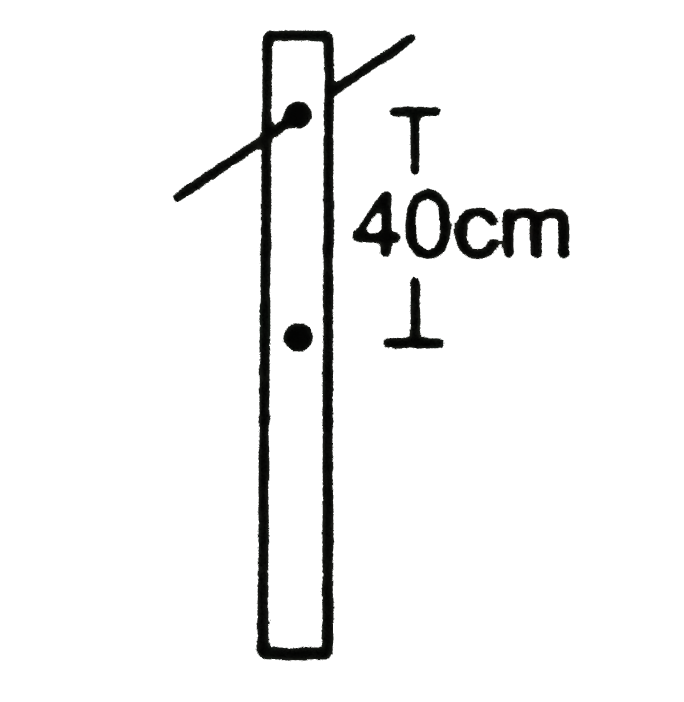
The seperation between the centre of mass of the stick and the point of suspension is d=40 cm. The time period of this physical pendulum is
T=2π√Imgd
=2π
⎷ml212+md2mgd
=2π⎡⎢
⎢⎣√112+0.164⎤⎥
⎥⎦⎞⎟
⎟⎠s=1.55s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Knowledge Check
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
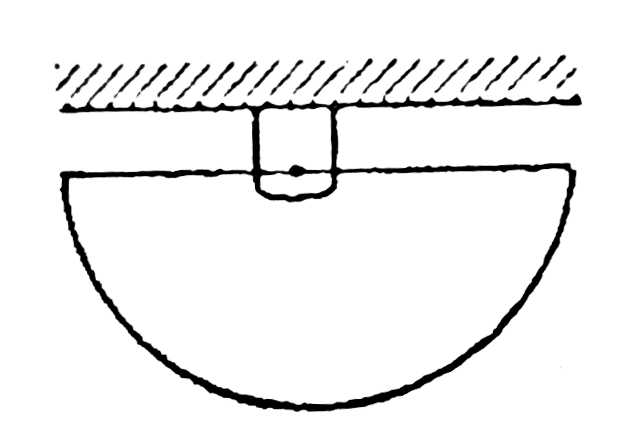 A2π√3r8gB2π√3rπ8gC2π√2rπ9gD2π√2r9g
A2π√3r8gB2π√3rπ8gC2π√2rπ9gD2π√2r9gA square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.
 A2π√2a3gB2π√√2a3gC2π√2√2a3gD2π√2√2ag
A2π√2a3gB2π√√2a3gC2π√2√2a3gD2π√2√2ag
A simple pendulum of length l is suspended throught the ceiling of an elevator. Find the time period of small oscilations if the elevator a. is going up with an acceleration a0. b. is going down with an acceleration a0 and c. is moving with a uniform velocity.
View SolutionA uniform disc of radius r is to be suspended through a small hole made in te disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
View SolutionIn the diagram shown find the time period of pendulum for small oscillations
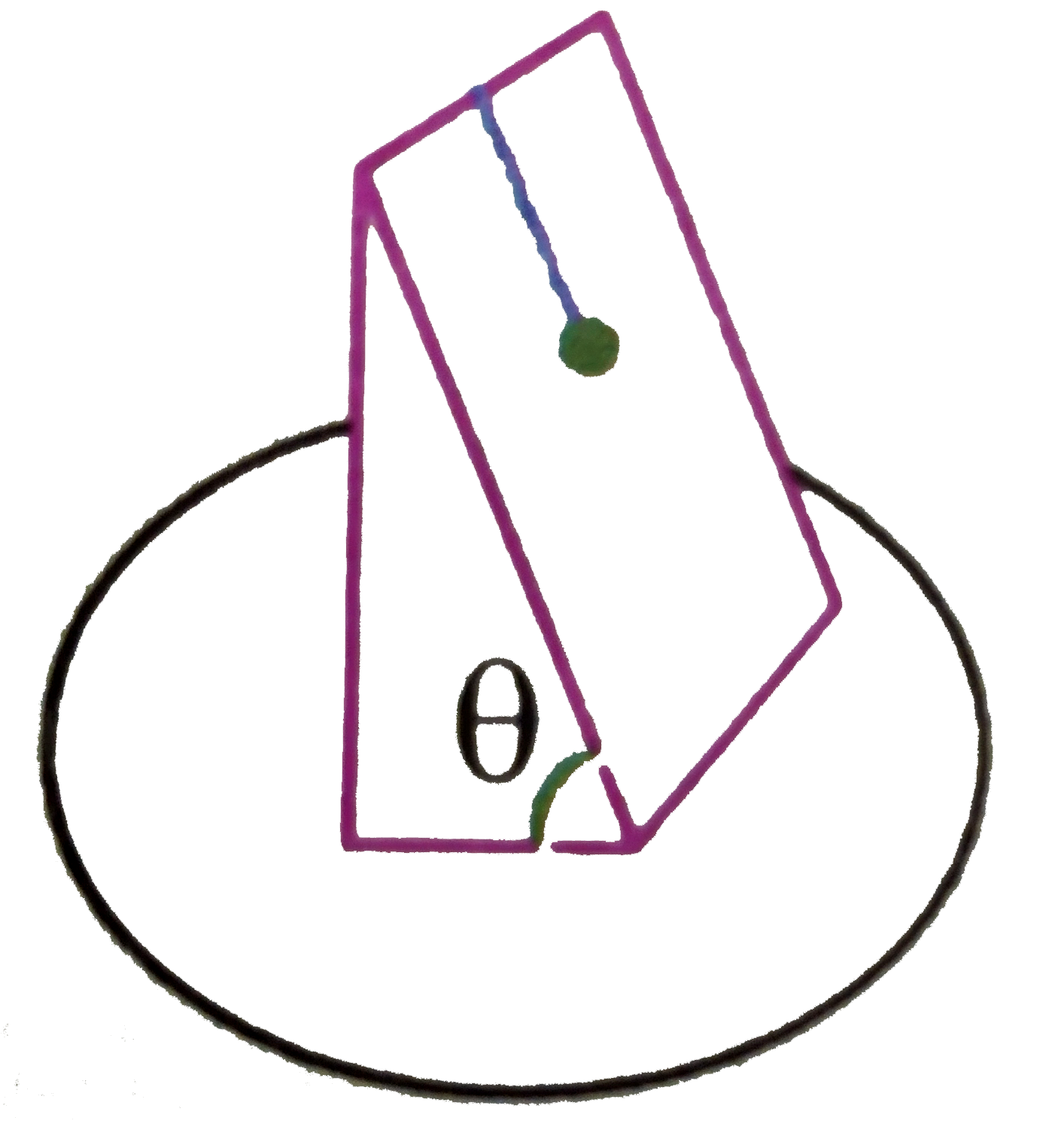
View SolutionA simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionFind the time period of m if pulley P is light and small.
View Solution