A uniform metre stick of mass 200 g is suspended from the ceiling through two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from the left end. Find the tensions in the two strings.
The correct Answer is:A, B, D
To solve the problem of finding the tensions in the two strings supporting a uniform meter stick with an additional mass, we can follow these steps:
Step 1: Identify the Forces Acting on the System
- The meter stick has a mass M=200g=0.2kg.
- The small object has a mass m=20g=0.02kg.
- The weight of the meter stick acts downwards at its center of mass (50 cm from the left end).
- The weight of the small object acts downwards at 70 cm from the left end.
- The tensions in the strings are T1 (left string) and T2 (right string).
Step 2: Write the Equilibrium Conditions
Since the system is in equilibrium, the sum of the vertical forces must equal zero:
T1+T2=Mg+mg
Substituting the values:
T1+T2=(0.2kg⋅9.8m/s2)+(0.02kg⋅9.8m/s2)
Calculating the weights:
T1+T2=1.96N+0.196N=2.156N(Equation 1)
Step 3: Calculate the Torque About One End
To find the tensions, we can take moments about the left end (where T1 acts). The sum of the torques must also equal zero:
T2⋅100cm=Mg⋅50cm+mg⋅70cm
Substituting the values:
T2⋅100=(0.2⋅9.8⋅50)+(0.02⋅9.8⋅70)
Calculating the right-hand side:
T2⋅100=(0.2⋅9.8⋅50)+(0.02⋅9.8⋅70)=0.2⋅9.8⋅50+0.02⋅9.8⋅70
=0.2⋅490+0.02⋅686=98+13.72=111.72N \cdot cm
Now, solving for T2:
T2=111.72100=1.1172N≈1.12N
Step 4: Substitute T2 Back into Equation 1
Now we can substitute T2 back into Equation 1 to find T1:
T1+1.12=2.156
Solving for T1:
T1=2.156−1.12=1.036N≈1.04N
Final Answer
Thus, the tensions in the two strings are:
- T1≈1.04N
- T2≈1.12N
- The meter stick has a mass M=200g=0.2kg.
- The small object has a mass m=20g=0.02kg.
- The weight of the meter stick acts downwards at its center of mass (50 cm from the left end).
- The weight of the small object acts downwards at 70 cm from the left end.
- The tensions in the strings are T1 (left string) and T2 (right string).
Since the system is in equilibrium, the sum of the vertical forces must equal zero:
T1+T2=Mg+mg
Substituting the values:
T1+T2=(0.2kg⋅9.8m/s2)+(0.02kg⋅9.8m/s2)
Calculating the weights:
T1+T2=1.96N+0.196N=2.156N(Equation 1)
To find the tensions, we can take moments about the left end (where T1 acts). The sum of the torques must also equal zero:
T2⋅100cm=Mg⋅50cm+mg⋅70cm
Substituting the values:
T2⋅100=(0.2⋅9.8⋅50)+(0.02⋅9.8⋅70)
Calculating the right-hand side:
T2⋅100=(0.2⋅9.8⋅50)+(0.02⋅9.8⋅70)=0.2⋅9.8⋅50+0.02⋅9.8⋅70
=0.2⋅490+0.02⋅686=98+13.72=111.72N \cdot cm
Now, solving for T2:
T2=111.72100=1.1172N≈1.12N
Now we can substitute T2 back into Equation 1 to find T1:
T1+1.12=2.156
Solving for T1:
T1=2.156−1.12=1.036N≈1.04N
Thus, the tensions in the two strings are:
- T1≈1.04N
- T2≈1.12N
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
A small stone of mass 50 g is rotated in a vertical circle of radius 40 cm. What is the minimum tension in the string at the lowest point?
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
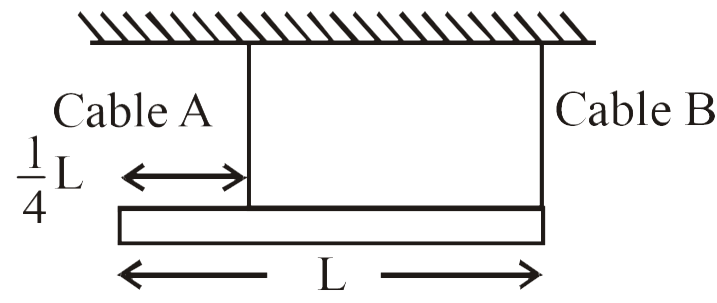 View Solution
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View Solution
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling . The rod is of mass 'm' and has another weight of mass 2 m hung at a distance of 75 cm from A . The tension in the string at A is :View SolutionA pendulum bob of mass 50 gm is suspended from the ceiling of an elevator. The tension in the string if the elevator goes up with uniform velocity is approximately
View SolutionA small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 View Solution
View SolutionA light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are μ and 9μ and the tension is T. Find the possible values of frequencies such that junction of two wire point A is a node.
 View Solution
View Solution

