A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
To find the tensions in the two strings, we will analyze the forces acting on each block separately.
1. Identify the Masses and Forces:
- Let the mass of the first block (m1) = 0.2 kg.
- Let the mass of the second block (m2) = 0.3 kg.
- The acceleration due to gravity (g) = 10 m/s².
2. Free Body Diagram for the Second Block (m2):
- For the second block (m2 = 0.3 kg), the forces acting on it are:
- Weight (downward): W2=m2⋅g=0.3⋅10=3N
- Tension in the string (upward): T2
- According to Newton's second law, the net force acting on m2 is:
T2=W2
- Therefore, we have:
T2=3N
3. Free Body Diagram for the First Block (m1):
- For the first block (m1 = 0.2 kg), the forces acting on it are:
- Weight (downward): W1=m1⋅g=0.2⋅10=2N
- Tension in the string from the ceiling (upward): T1
- Tension from the second block (downward): T2
- The equation of motion for m1 can be written as:
T1=W1+T2
- Substituting the values we have:
T1=2N+3N=5N
4. Final Results:
- The tension in the first string (T1) is 5N.
- The tension in the second string (T2) is 3N.
Summary:
- Tension in the first string (T1) = 5 N
- Tension in the second string (T2) = 3 N
- Let the mass of the first block (m1) = 0.2 kg.
- Let the mass of the second block (m2) = 0.3 kg.
- The acceleration due to gravity (g) = 10 m/s².
- For the second block (m2 = 0.3 kg), the forces acting on it are:
- Weight (downward): W2=m2⋅g=0.3⋅10=3N
- Tension in the string (upward): T2
- According to Newton's second law, the net force acting on m2 is:
T2=W2
- Therefore, we have:
T2=3N
- For the first block (m1 = 0.2 kg), the forces acting on it are:
- Weight (downward): W1=m1⋅g=0.2⋅10=2N
- Tension in the string from the ceiling (upward): T1
- Tension from the second block (downward): T2
- The equation of motion for m1 can be written as:
T1=W1+T2
- Substituting the values we have:
T1=2N+3N=5N
- The tension in the first string (T1) is 5N.
- The tension in the second string (T2) is 3N.
- Tension in the first string (T1) = 5 N
- Tension in the second string (T2) = 3 N
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -29videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions64videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
Similar Questions
The block of mass m is at rest. Find the tension in the string A .
 View Solution
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
 View Solution
View SolutionA block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is
 View Solution
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)
 View Solution
View SolutionA block of mass 2kg is suspended through two light spring balances A and B. Then A and B will read respectively
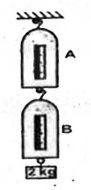 View Solution
View SolutionA wooden block of mass 0.8 kg is dragged along a level frictionless surface by a hanging block of mass 0.2 kg as shown in the figure. Calculate the tension in the string and the acceleration of blocks.
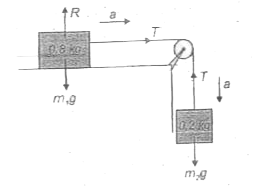 View Solution
View SolutionIn the figure a block of mass 10kg is in equilibrium. Identify the string in which the tension is zero
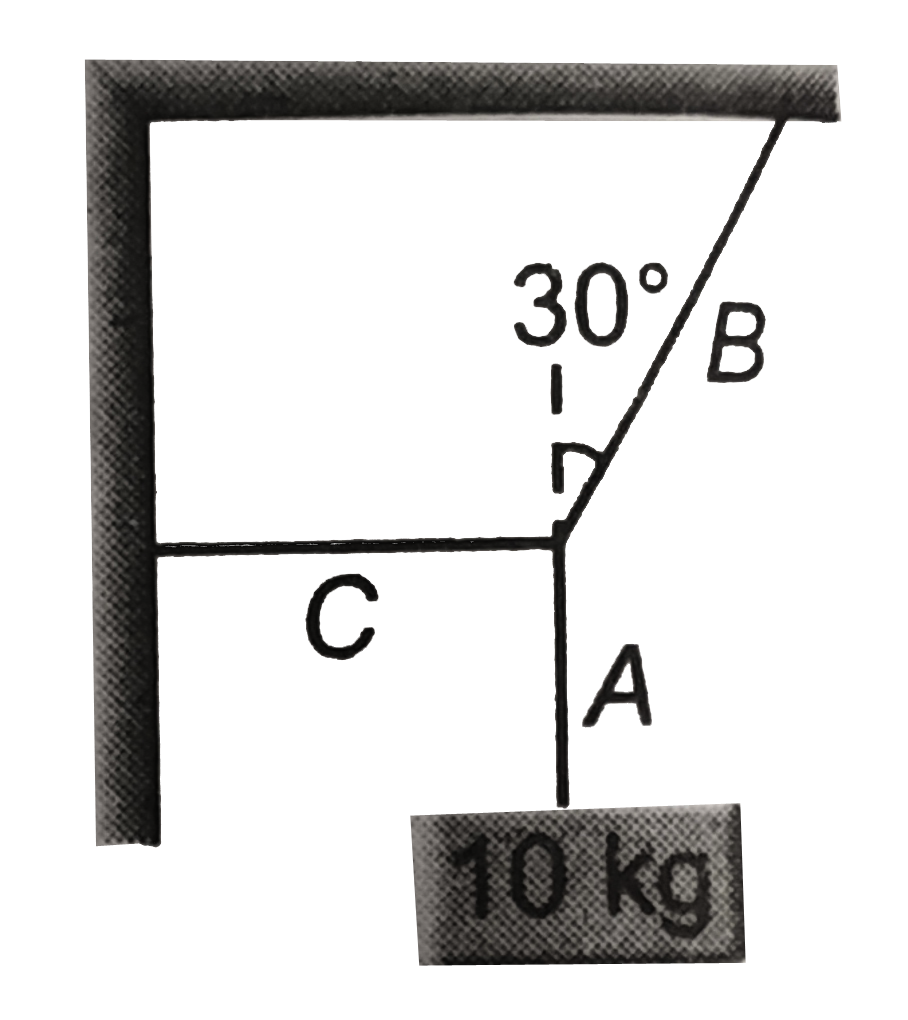 View Solution
View SolutionA wooden block of mass 0⋅8 kg is dragged along a level frictionless surface by a hanging block of mass 0⋅2 kg as shown in the figure . Calculate the tension in the string and the acceleration of blocks .
 View Solution
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View Solution

