A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
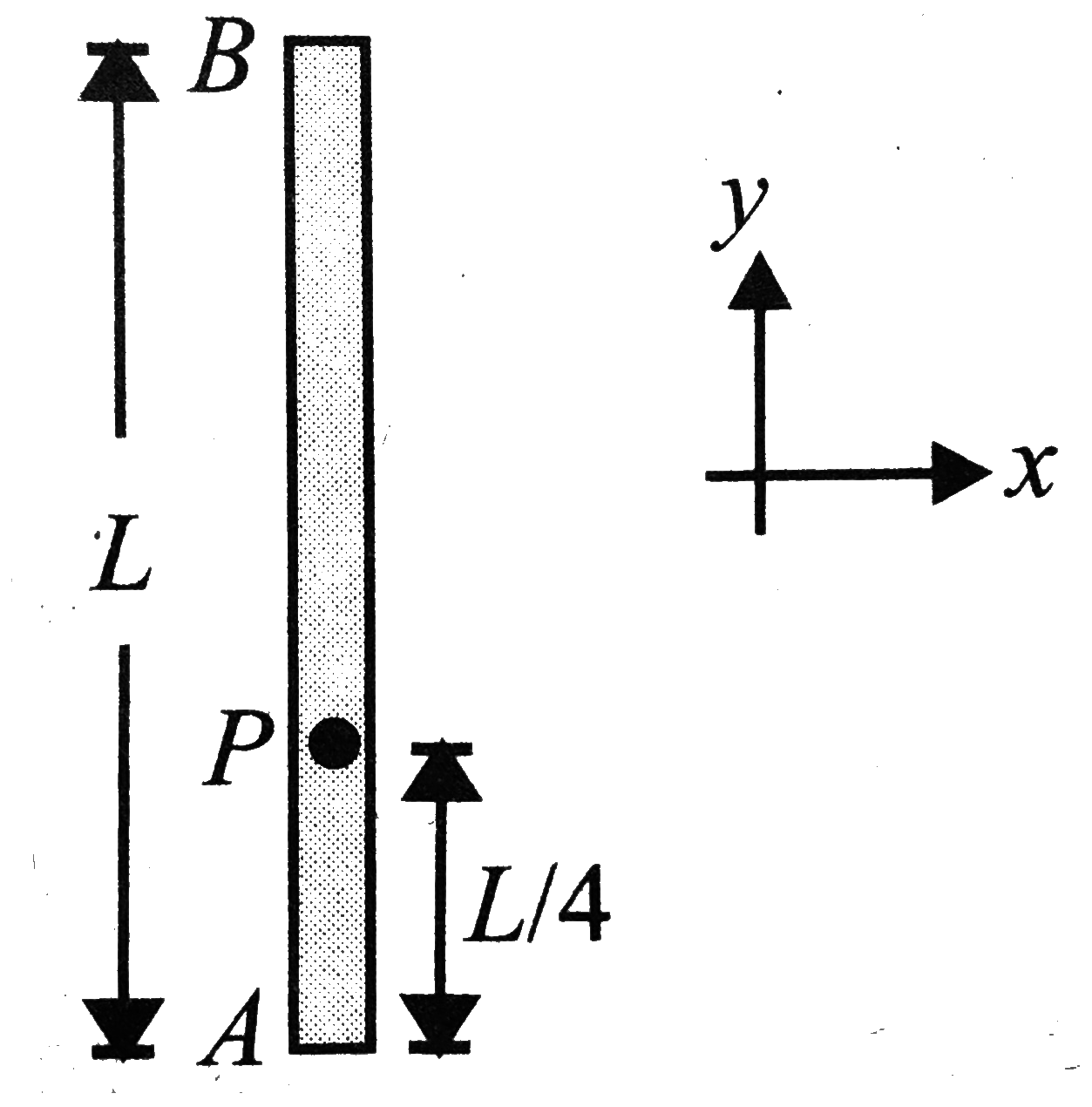
The acceleration of the centre of mass of the rod is
−6g7ˆi−12g7ˆj
−12g7ˆi−6g7ˆj
−3g7ˆi−9g7ˆj
−9g7ˆi−3g7ˆj
The correct Answer is:A
From conservation of energy we get
mgl4=12m[l212+l216]ω2,ω2=24g7l
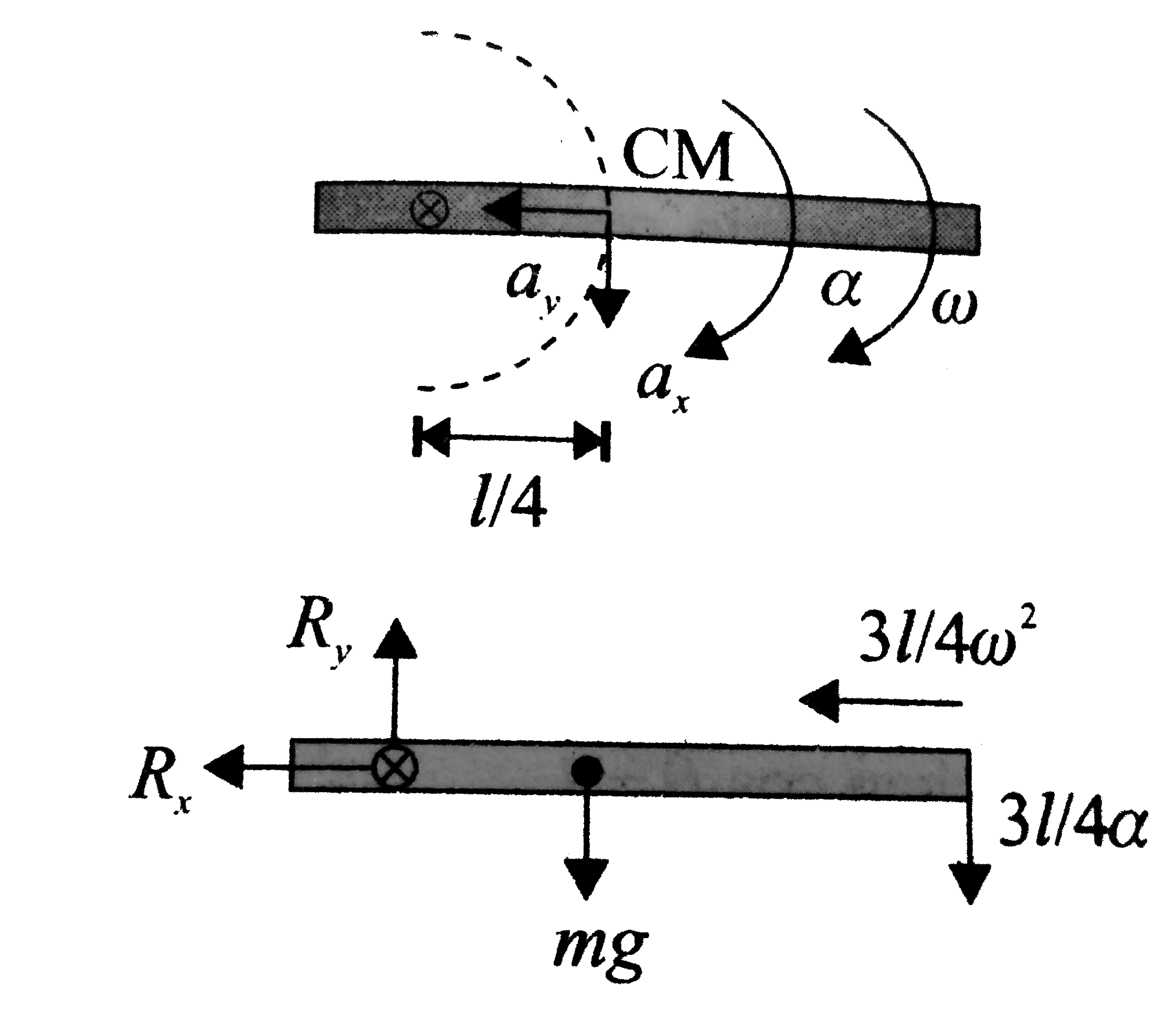
From Newton's law
mgl4=(ml212+ml216)α……….i
mg−Ry=m(14α) ………….ii
Rx=ml4ω2..........iii
α=12g7l,→aCM=−ω2l4ˆi−14αˆj
=6g7ˆi−3g7ˆj
→aB=−ω2(3l4)ˆi−(3l4)αˆj
→Rx=−6mg7ˆi,→Rh=+4mg7ˆj
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
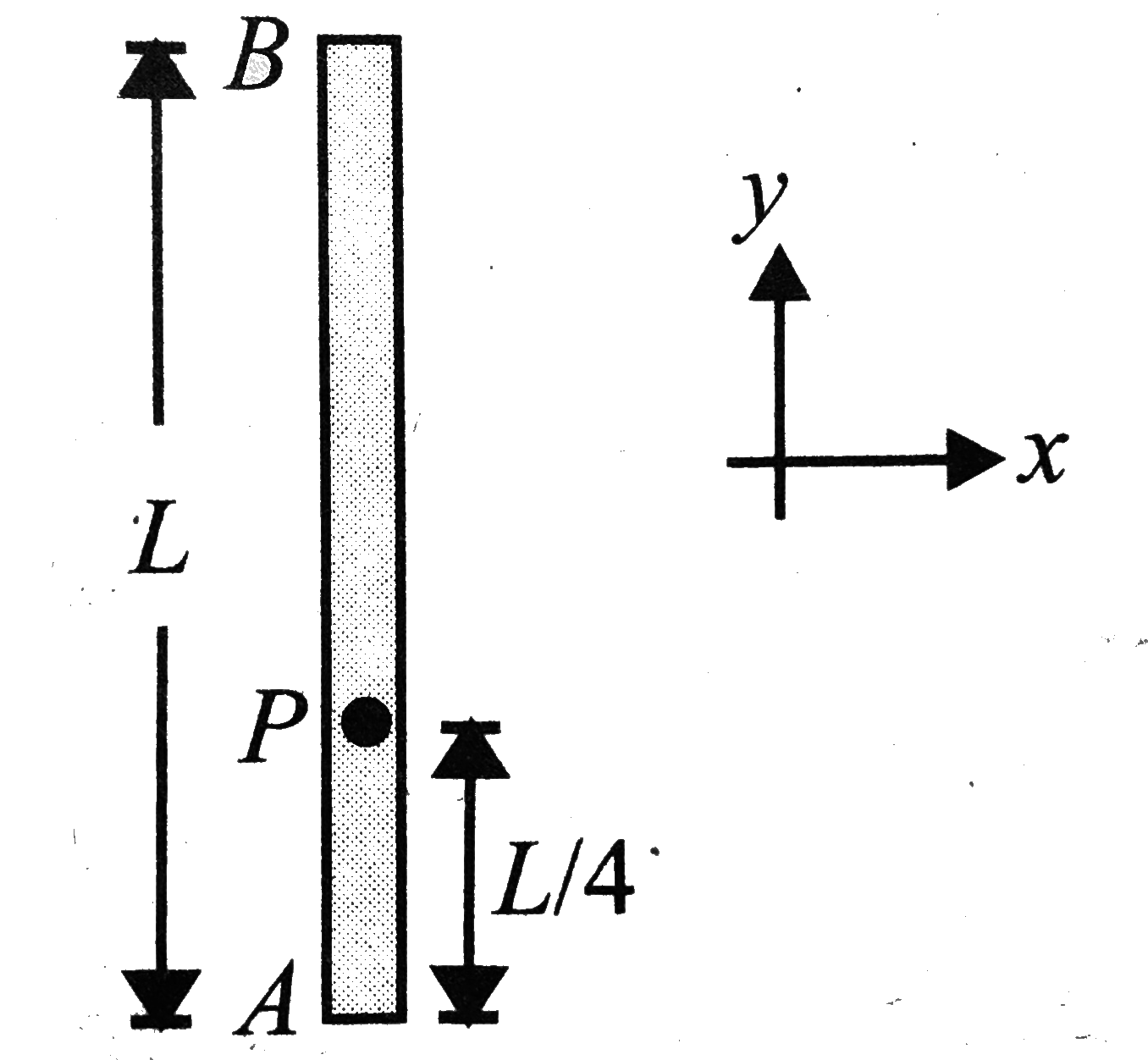
The acceleration of end B of the rod isView SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
 View Solution
View SolutionA uniform rod is rotating about a horizontal axis as shown. The rod is hinged at one of the ends. The rod is released from a vertical position by slightly pushing it. As the rod moves from A to B
 View Solution
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 View Solution
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
 View Solution
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA uniform rod of length 75cm is hinged at one of its ends and is free to rotate in vertical plane. It is released from rest when rod is horizontal. When the rod becomes vertical, it is breaks at mid− point and lower part now moves freely. The distance of centre of lower part from hinge, when it again becomes vertical for the first time is r. Find the approximate value of 2r.
View Solution

