A uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
2λgL2Al
λgL22Al
2λgLAl
λgl2AL
The correct Answer is:B
To find the Young's modulus of a uniform rod of length L, mass per unit length λ, cross-sectional area A, and elongation l due to its own weight when suspended from the ceiling, we can follow these steps:
1. Identify the Forces Acting on the Rod:
The rod is suspended vertically, and the force acting on a small section of the rod at a distance x from the free end is due to the weight of the portion of the rod below that point. The weight of the section below x is given by:
F=λ(L−x)g
where g is the acceleration due to gravity.
2. Calculate the Stress at Section x:
Stress (σ) at the section x is defined as the force acting on the section divided by the area of cross-section A:
σ=FA=λ(L−x)gA
3. Determine the Strain in the Section:
The elongation dL of the small section dx can be expressed in terms of stress and Young's modulus (Y):
dL=σ⋅dxY=λ(L−x)g⋅dxAY
4. Integrate to Find Total Elongation:
To find the total elongation l of the rod, integrate dL from x=0 to x=L:
l=∫L0λ(L−x)g⋅dxAY
5. Evaluate the Integral:
The integral can be simplified:
l=λgAY∫L0(L−x)dx
The integral ∫L0(L−x)dx=(Lx−x22)L0=L2−L22=L22.
Thus,
l=λgAY⋅L22
6. Rearranging for Young's Modulus:
Rearranging the equation to solve for Young's modulus Y:
Y=λgL22Al
Final Expression for Young's Modulus:
The Young's modulus of the rod is given by:
Y=λgL22Al
The rod is suspended vertically, and the force acting on a small section of the rod at a distance x from the free end is due to the weight of the portion of the rod below that point. The weight of the section below x is given by:
F=λ(L−x)g
where g is the acceleration due to gravity.
Stress (σ) at the section x is defined as the force acting on the section divided by the area of cross-section A:
σ=FA=λ(L−x)gA
The elongation dL of the small section dx can be expressed in terms of stress and Young's modulus (Y):
dL=σ⋅dxY=λ(L−x)g⋅dxAY
To find the total elongation l of the rod, integrate dL from x=0 to x=L:
l=∫L0λ(L−x)g⋅dxAY
The integral can be simplified:
l=λgAY∫L0(L−x)dx
The integral ∫L0(L−x)dx=(Lx−x22)L0=L2−L22=L22.
Thus,
l=λgAY⋅L22
Rearranging the equation to solve for Young's modulus Y:
Y=λgL22Al
The Young's modulus of the rod is given by:
Y=λgL22Al
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod is
View SolutionA copper rod length L and radius r is suspended from the ceiling by one of its ends. What will be elongation of the rod due to its own weight when p andYare the density and Young's modulus of the copper respectively?
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionThe centre of mass of a non-uniform rod of length L whose mass per unit length λ is proportional to x2, where x is distance from one end
View Solutionwire of length I has a ear mass density λ and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight
View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionA wire of natural length l, young's modulus Y and area of cross-section A is extended by x. Then, the energy stored in the wire is given by
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
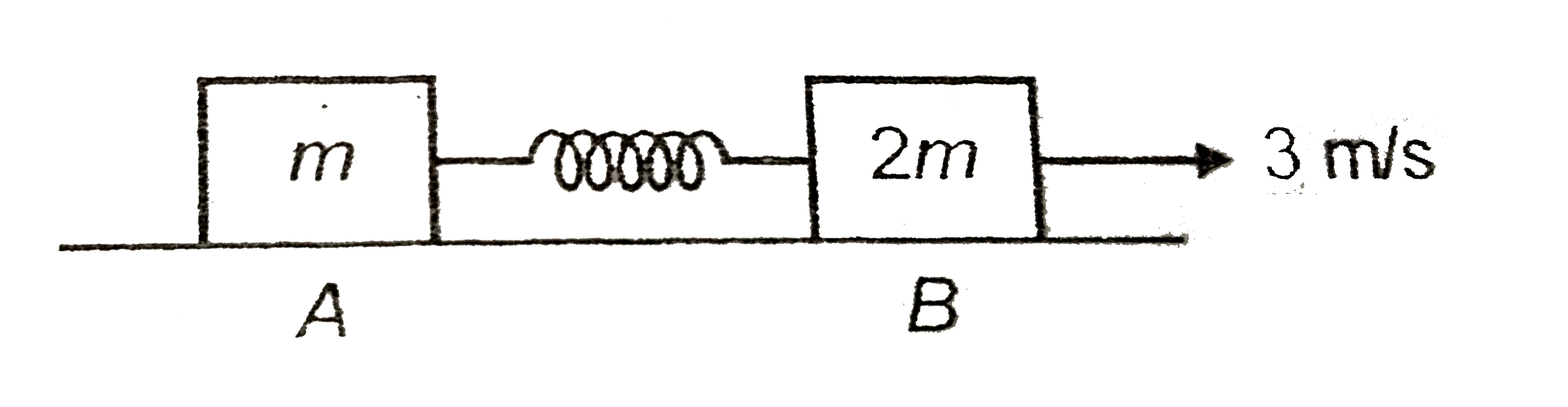
View Solution
