
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring is
2π ⎷rg(1+1π2)
2π ⎷rg(1+4π2)12
2π ⎷rg(1−2π2)12
2π ⎷2rg(1+4π)12
The correct Answer is:D

T=2π√I0mgd,I0=Ic+mr'2⇒mr2=IC+mr'2
⇒IC=m(r2−r'2)
I0=IC+md2m(r2−r'2)+m(r2+r'2)=2mr2
d=√r2(2rπ)2=r√1+4π2
T=2π
⎷2rg(1+4π)12
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View Solution
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA uniform current carrying ring of mass m and radius R is connected by a massless string as shown in Fig. 1.142. A uniform magnetic field B0 exists in the region to keep the ring in horizontal position, then the current in the ring is (l=length of string)
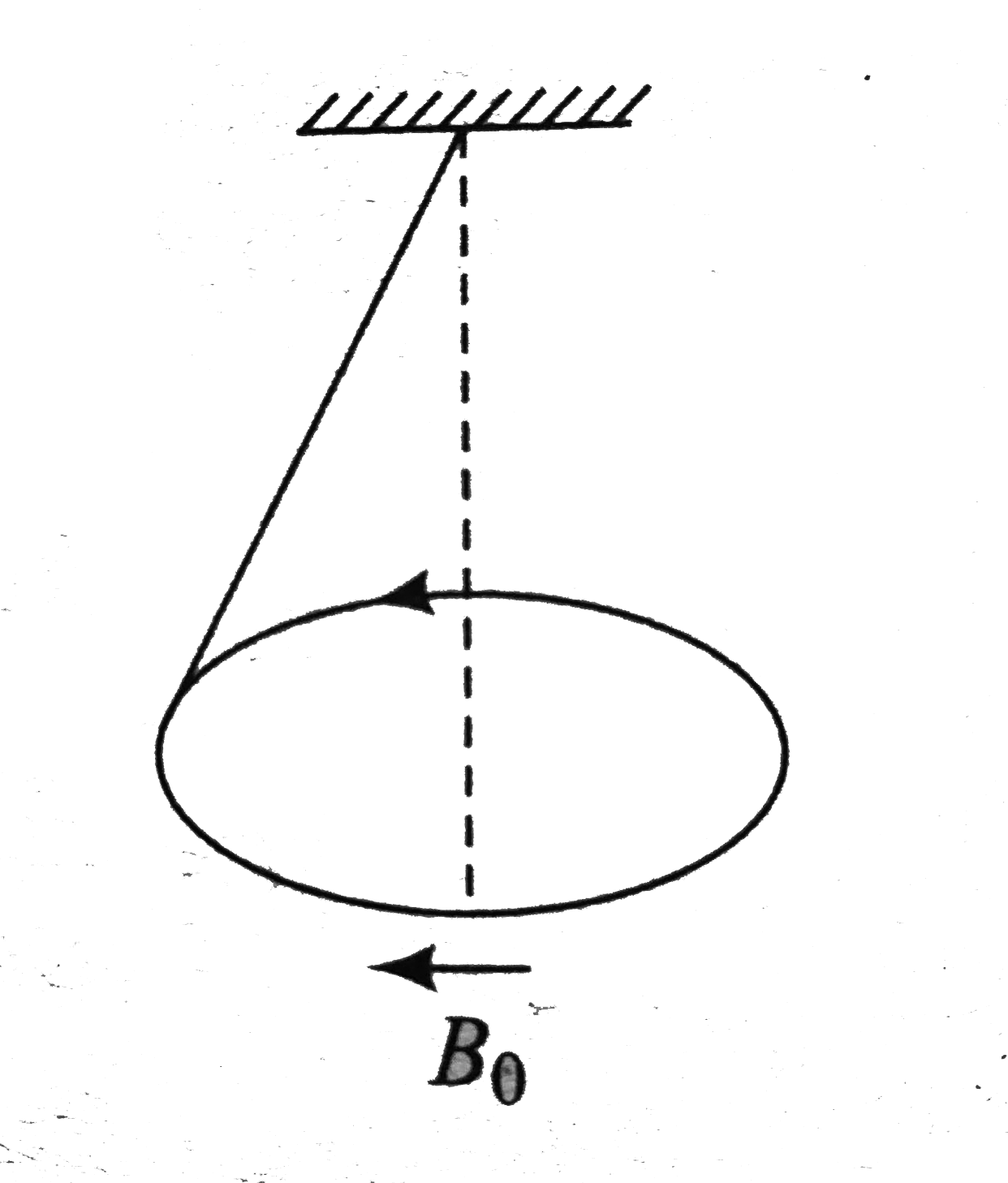 .AmgπRB0BmgRB0Cmg3πRB0DmglπR2B0
.AmgπRB0BmgRB0Cmg3πRB0DmglπR2B0A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
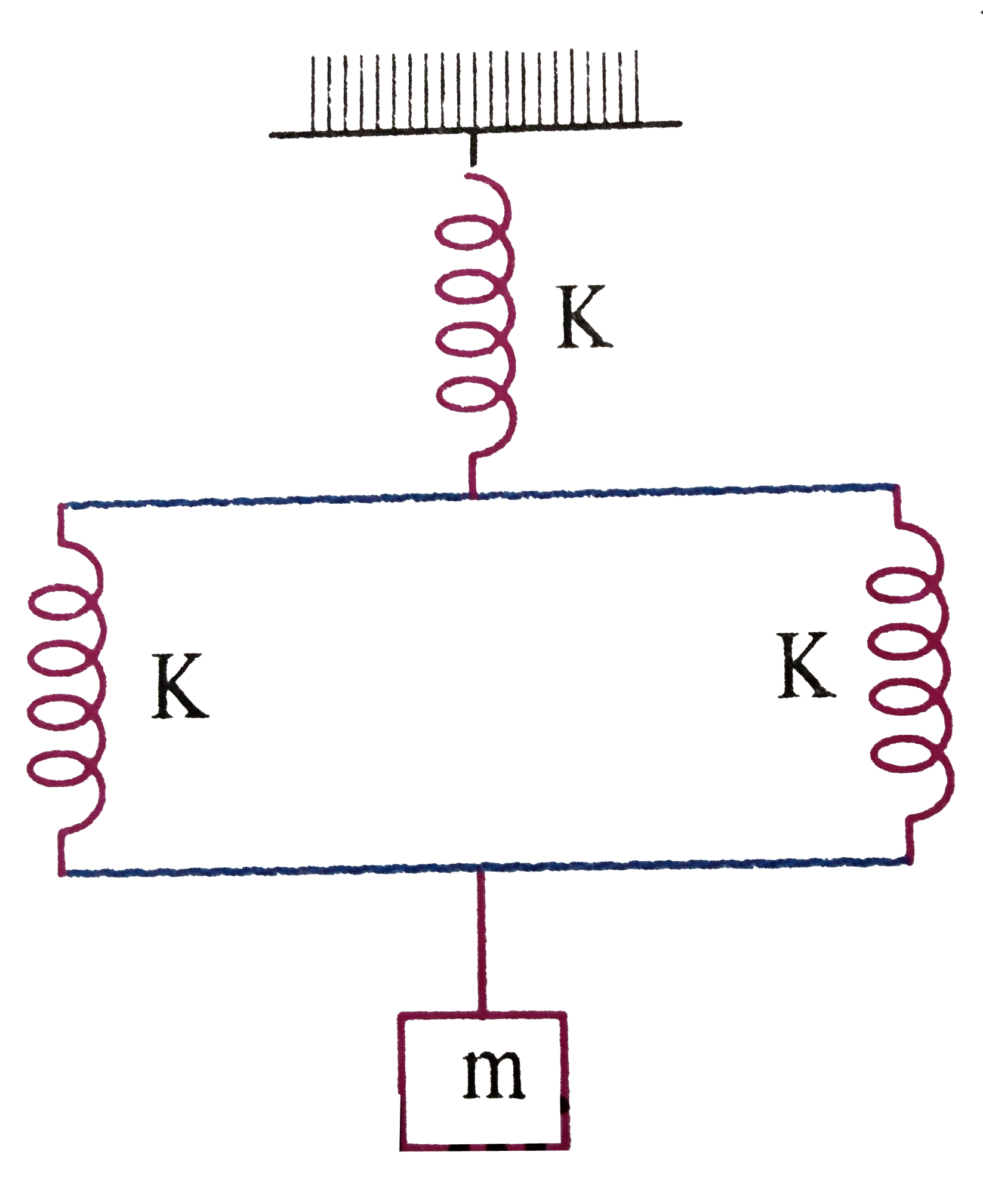 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
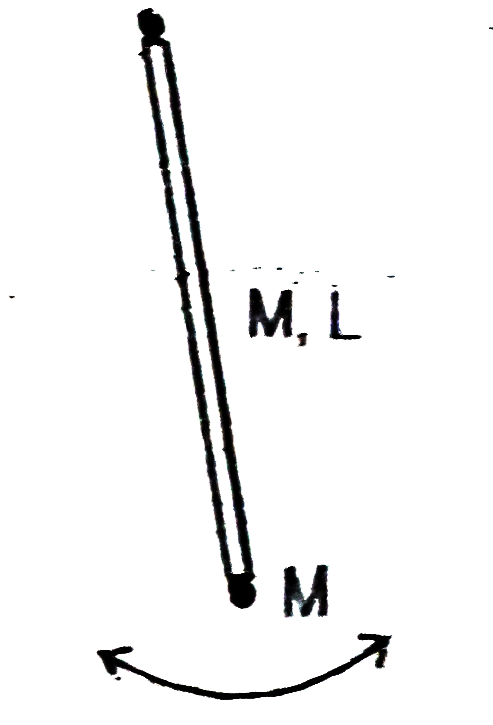
View SolutionA ring is oscillating about a horizontal axis passes through its rim. Determine time period of oscillation.
View SolutionA half ring of mass m, radius R is hanged at its one end its one end in verical plane and if free to socilalte in its plane.
Find oscillations frequency of the half ring.
_E01_109_Q01.png)
View SolutionThere is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
View Solution
