A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is pulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?


μMg
2μMg
3μMg
4μMg
The correct Answer is:c
Let a be the acceleration of the center of the mass of disc. Then Ma=F−f………(i)
If there is no slipping, angular acceleration of the disc,
α=aR
Now torque of the disc τ=Iα=Rf
or τ=(12MR2)α=Rf ∴ For a disc I=12MR2
∴(12MR2)(aR)=Rf⇒Ma=2f (using (ii))
Substituting this in Eq. (i), we get
2f=F-f or f=F3
Since, there is no slipping,
∴f≤μMg⇒F≤3μMg∴Fmax=3μMg

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ANGULAR MOMENTUM IN CASE OF ROTATIONS ABOUT A FIXED AXIS
16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION
16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - KENEMATICS OF ROTATIONAL MOTION ABOUT A FIXED AXIS
3 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
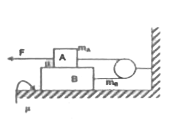
Two blocks A and B are lying on the table as shown in the figure. The coefficient of friciton between block A and block B is μ. The coefficient of friction between block B and ground also μ. An external force F is applied in the direction shown. The maximum value of the force F that can be applied without moving the blocks.
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
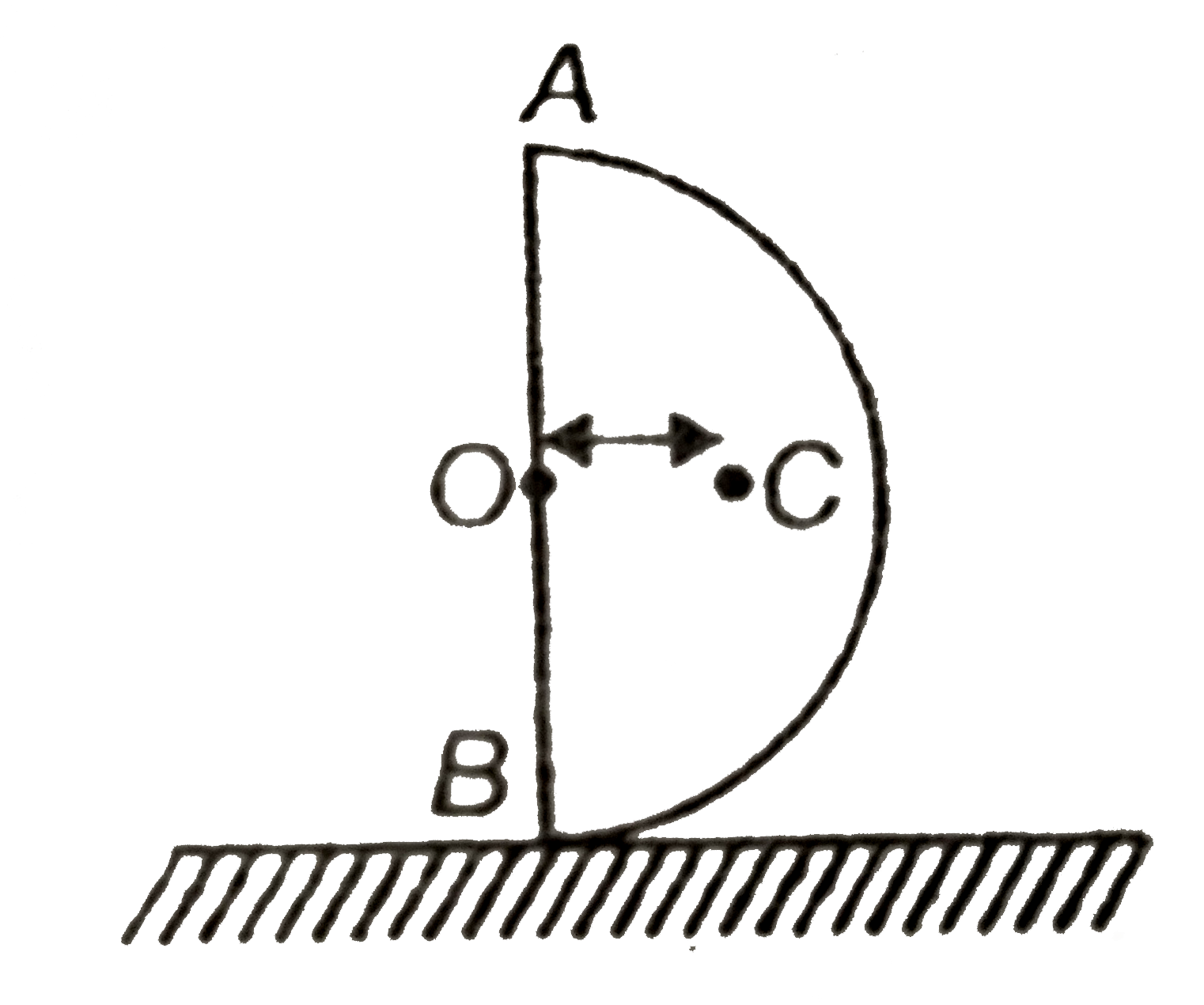
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA uniform disc of radius r and mass m is free to rotate on a frictionless pivot through point P on its rim as shown in Fig. The disc is at rest and is released from the position (1). (i) What is the speed of the centre of mass when the disc reaches the position (2). (ii) Also rind the speed of the lowest point on the disc in the dashed position.

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

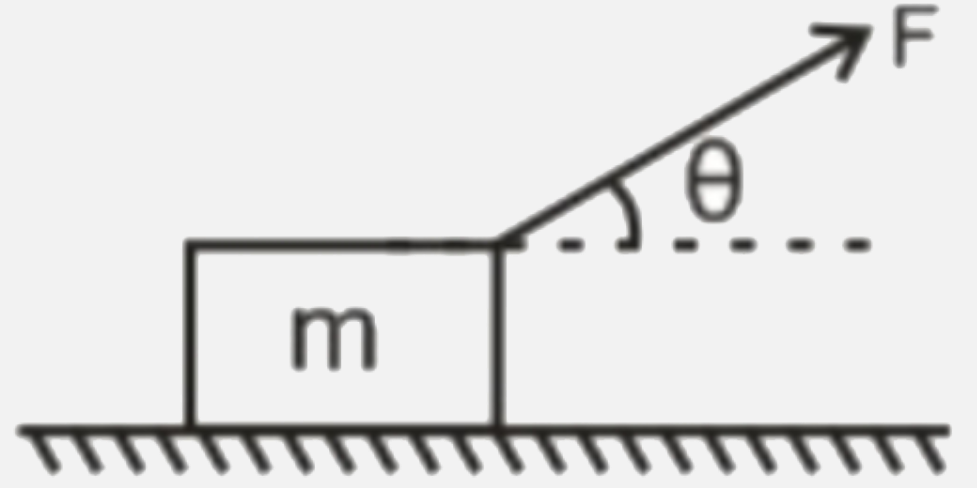
View SolutionA wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
View Solution