A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rads−2 in the wheel. Calculate the moment of inertia of the wheel.
 Solution in Tamil
Solution in Tamil
The forces acting on the wheel are i. W due to gravity ii N due to the support at the cnetre and iii F due to tension. The torque of W and N are separately zero and that of F is F.r. The net torque is
Γ=(5.0N).(10cm)=0.50N.m.
The moment of inertia is
I=Γa=0.50N−m2rads62=0.25kg−m2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples
29 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
22 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A wheel rotates with a constant acceleration of 2.0rads2. If the wheel starts from rest, how many revolutions will it make in the first 10 seconds?
View SolutionCan an object be in pure translation as well as in pure rotation?
View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 nd radius 20 cm. The wheel is free to rotate about it axis. Initially, thewheel is t rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA constant torque of 31.4N−m is exterted on a pivoted wheel. If the angular acceleration of the wheel is 4πrad/s2, then the moment of inertia will be.
View SolutionA wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung. An angular acceleration of 8 rad//s^(2) is produced in it due to the torque. Then, the moment of inertia of the wheel is ( g=10m//s^(2) )
View SolutionA constant torque of 31.4 Nm is applied to a pivoted wheel. If the angular acceleration of the wheel is 2pi" rad/s"^(2) , then its moment of inertia is
View SolutionA constant torque of 3.14 N.m is exerted on a pivoted wheel. If the angular acceleration of the wheel is 4pi"rad".s^(-2) , then the moment of inertia of the wheel is
View SolutionA torque of 3.14 N .m constant is applied to a wheel rotating with a mass on the pivot. If the angular acceleration of the wheel is 4 rad / s ^ 2 then what will be the inertia of the wheel?
View Solutionचित्रानुसार, 0.4m त्रिज्या का एक पहिया अपने अक्ष के परितः मुक्त रूप से घूर्णन कर सकता है। एक डोरी को इसकी रिम पर लपेटा गया है तथा इसके सिरे पर 4kg द्रव्यमान लटकाया गया है। बल आघूर्ण के कारण इसमें 8rad−s−2 का कोणीय त्वरण उत्पन्न होता है। तब पहिये का जड़त्व आघूर्ण होगा (g=10ms−2)

View Solution31.4 N - m का एक नियत बल आघूर्ण एक कीलकित पहिए पर आरोपित किया जाता है। यदि पहिए का कोणीय त्वरण 4πrad/sec2 हो, तो पहिए का जड़त्व आघूर्ण है
View Solution0.20Kg−m2 जड़त्व आघूर्ण और 20 cm त्रिज्या वाले पहिये की परिधि पर एक डोरी लपेटी गई है। पहिया F = 20 N बल से खींचा जाता है। 5 सेकण्ड के पश्चात् पहिये का कोणीय वेग का मान रेडियन/सेकंड मे ज्ञात कीजिये।
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad s−2 is produced in it due to the torque. Then moment inergia of the wheel is (g = 10ms−2)
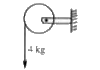
View SolutionA wheel of radius 20 cm can rotate about its centre. A string is wrapped over its rim and is pulled by a force of 10N tangential to pulley. If the angular acceleration produced is 4 rad s−2 then the moment of inertia of the wheel in kg m2 is
View Solution
