A YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
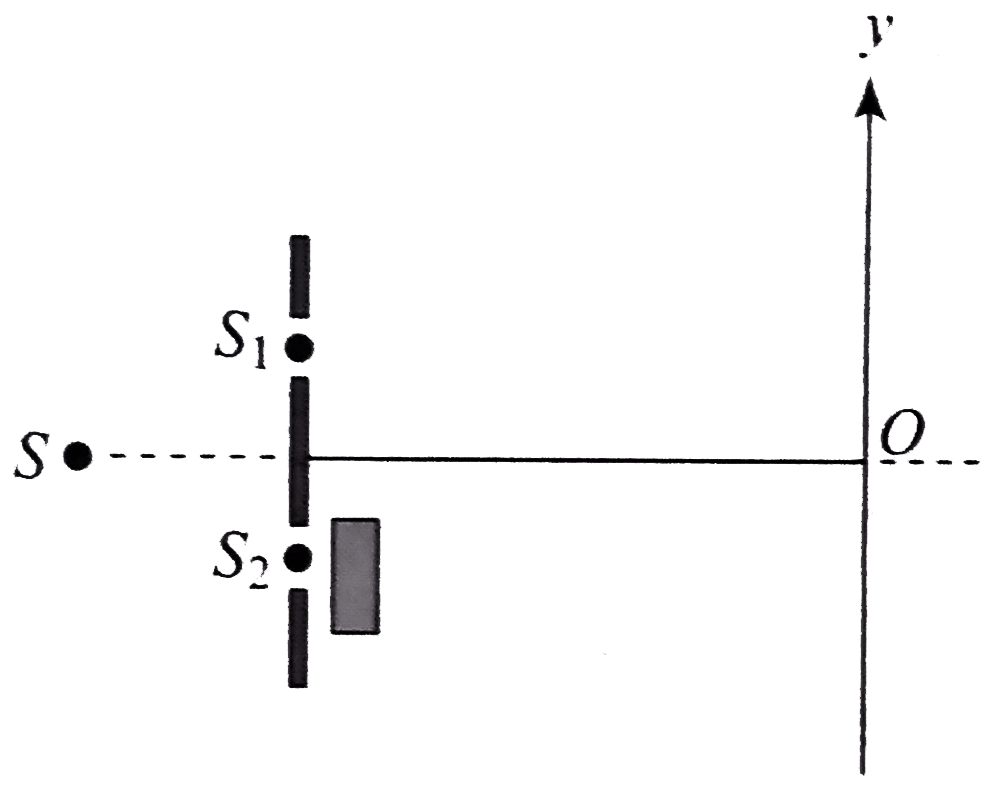
Find the light intensity at point O relative t maximum fringe intensity.
14Imax
54Imax
12Imax
34Imax
The correct Answer is:a
Path difference at point P on the screen, Δx=ydD
At the position of central maxima, the optical path length S2P and S1P and equal.
(S2P−t)c/μ1=1c/μ2=S1Pc/μ1
where μ1=4/3,μ2=3/2.
μ1(S1P−S2P)=(μ2−μ)t
μ1(ydD)=(μ2−μ1)t
y=(μ2−μ1)tDμ1d
=[(3/2)−(4/3)]×10.4×1.5(4.3)×0.45×10−3=4.33mm

b. At point O, net path difference.
Δx=(μ2μ1−1)t
Net phase difference,
Δϕ=2πλΔx
=2π6×10−7(1.54/3−1)(10.4×10−6)=(133)π
Thus, intensity
I=Imaxcos2(ϕ/2)
=Imaxcos2(13π6)=34Imax
c. For maximum intensity at point O,
Δx=nλ
Path difference at point O,
Δx=(1.54/3−1)(10.4×10−6)=1300nm
Thus, maximum intensity will correspond to 13002nm,
13003nm,...
In the given range, required values are 650 nm and 433.33 nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
View SolutionA light wave of frequency 5×1014Hz enters a medium of refractive index 1.5. In the velocity of the light wave is ….. And its wavelength is ……
View SolutionStatement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zero
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
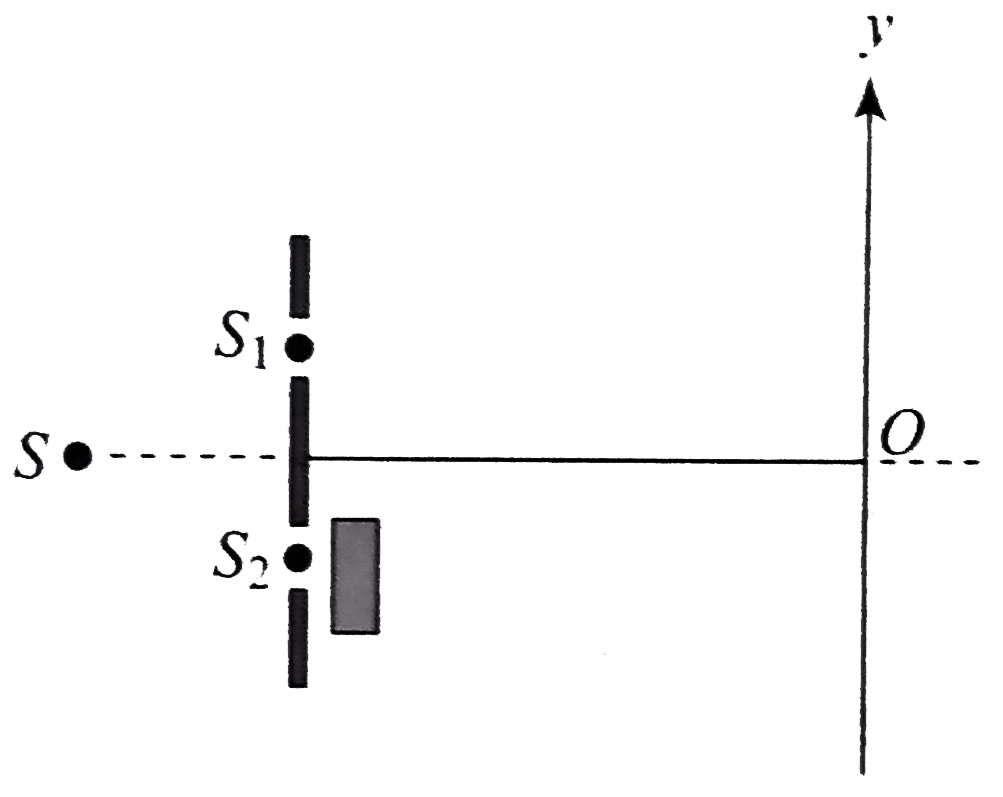
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionA YDSE is performed in a medium of refractive index 4 // 3 , A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S_(2) is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4 // 3 , ignore absorption.) Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.
View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S_(2) is covered by a thin glass sheet of thickness 10.4 mum and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion. Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:
View SolutionThe young's slit experiment is done in a medium of refractive index 4//3 .A light of 600 nm wavelength is falling on the slits having 0.45 mm separation . The lower slit S_(2) is covered by a thin galss sheet of thickness 10.4 mum and r3efractive index 1.5 .The interferecnce pattern is observed on a screen placed 1.5 m form the slits as shown in figure .Find the light intensity at point O relative to the maximum fringle intensity (Given : cos3.4 =sqrt(0.75)
View Solutionयंग का द्वि - स्लिट प्रयोग 43अपवर्तनांक के माध्यम में किया जाता है | 600 नैनोमीटर तरंगदैर्ध्य का प्रकाश स्लिटों S1 व S2 पर जिनके बीच अंतराल 0.45 मिमी है, गिर रहा है | निचली स्लिट S2 काँच की पतली शीट से, जिसकी मोटाई 10.4 माइक्रोमीटर तथा अपवर्तनांक 1.5 है, ढकी गई है | व्यतिकरण प्रतिरूप, स्लिटों से 1.5 मी की दूरी पर रखे पर्दे पर देखा जाता है |
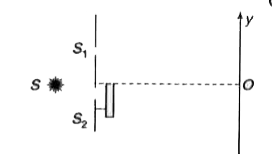
(a) Y- अक्ष पर केंद्रीय उच्चिष्ठ ( दीप्त फ्रिंज जिसके लिए पथांतर शून्य है ) की स्थिति ज्ञात कीजिए |
(b) बिंदु O पर, महत्तम फ्रिंज तीव्रता के सापेक्ष प्रकाश की तीव्रता ज्ञात कीजिए |
(c) अब यदि 600 नैनोमीटर के प्रकाश को 400 नैनोमीटर परास के श्वेत प्रकाश से बदल दिया जाए तो उस प्रकाश की तरंगदैर्ध्य ज्ञात कीजिए जो ठीक बिंदु पर उच्चिष्ठ बनाए (सभी तरंगदैर्ध्य, 4/3 अपवर्तनांक के दिए गए माध्यम के लिए हैं, विक्षेपण नगण्य हैं |)
View SolutionYoung’s double slit experiment is done in a medium of refractive index 4/3. Light of 600 nm wavelength is falling on the slits having 0.45 pm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 pm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown. (a) Find the location of central maxima (bright fringe with zero I t y path difference) on the y-axis. (b) Find the light intensity at point O relative to the maximum fringe intensity. (c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that from maxima exactly at point O[All wavelengths in this problem are for the given medium of refractive index 4/3 . Ignore dispersions.]
View SolutionThe young's double slit experiment is done in a medium of refractive index 4/3 . A light of 600 nm wavelength is falling on the slits having 0.45 mm separation. The lower slit S_(2) is covered by a thin glass sheet of thickness 10.4 mu m and refractive index 1.5. The interference pattern is observed on a screen placed. 1.5 m from the slit as shown in figure. Find the light intensity at point O relative to the maximum fringe intensity
View SolutionThe Young.s double slit experiment is done in a medium of refractive index 4/3 . A light of 600 nm wavelength is falling on the slits having 0.45 mm separation . The lower slit S_(2) is covered by a thin glass sheet of thickness 10.4 mu m and refractive index 1.5 . The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure .Find the light intensity at point O relative to the maxmum fringe intensity
View SolutionYoung bi-slit experiments are performed in a medium with a 4/3 refractive index. 600nm wavelength light is incident on 0.45 mm gap slits. 10.4 mu The lower slit S is covered by a thin glass plate of m thickness and 1.5 refractive index. The articulation format is observed diagrammatically on a screen 1.5m from the slito. Find the position of the central superlative (bright fridge with zero transition) on the y-axis.
View SolutionYoung bi-slit experiments are performed in a medium with a 4/3 refractive index. 600nm wavelength light is incident on 0.45 mm gap slits. 10.4 mu The lower slit S is covered by a thin glass plate of m thickness and 1.5 refractive index. The articulation format is observed diagrammatically on a screen 1.5m from the slito. Find the intensity of light at a point O compared to the maximum fridge intensity.
View Solution
