An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
1.3×102s
2.1×10−2s
1.6×10−10s
2.9×10−9s
The correct Answer is:D
To solve the problem of an electron falling a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C, we can follow these steps:
Step 1: Understand the forces acting on the electron
The electron, being negatively charged, will experience a force in the direction opposite to the electric field. The force acting on the electron can be calculated using the formula:
F=eE
where:
- e is the charge of the electron (1.6×10−19C)
- E is the magnitude of the electric field (2×104N/C)
Step 2: Calculate the acceleration of the electron
Using Newton's second law, F=ma, we can find the acceleration a of the electron:
a=Fm=eEme
where:
- me is the mass of the electron (9.11×10−31kg)
Step 3: Substitute the values into the acceleration formula
Now, substituting the values into the formula for acceleration:
a=(1.6×10−19C)(2×104N/C)9.11×10−31kg
Step 4: Calculate the acceleration
Calculating the above expression:
a=3.2×10−159.11×10−31≈3.51×1015m/s2
Step 5: Use the kinematic equation to find the time taken
We can use the kinematic equation for uniformly accelerated motion:
h=12at2
Rearranging for time t:
t=√2ha
Step 6: Substitute the values for h and a
Given h=1.5cm=1.5×10−2m, we substitute:
t=√2×(1.5×10−2)3.51×1015
Step 7: Calculate the time taken
Calculating the above expression:
t=√3.0×10−23.51×1015≈√8.55×10−18≈2.93×10−9s
Final Answer
The time taken by the electron to fall a distance of 1.5 cm in the electric field is approximately:
t≈2.9×10−9s
---
The electron, being negatively charged, will experience a force in the direction opposite to the electric field. The force acting on the electron can be calculated using the formula:
F=eE
where:
- e is the charge of the electron (1.6×10−19C)
- E is the magnitude of the electric field (2×104N/C)
Using Newton's second law, F=ma, we can find the acceleration a of the electron:
a=Fm=eEme
where:
- me is the mass of the electron (9.11×10−31kg)
Now, substituting the values into the formula for acceleration:
a=(1.6×10−19C)(2×104N/C)9.11×10−31kg
Calculating the above expression:
a=3.2×10−159.11×10−31≈3.51×1015m/s2
We can use the kinematic equation for uniformly accelerated motion:
h=12at2
Rearranging for time t:
t=√2ha
Given h=1.5cm=1.5×10−2m, we substitute:
t=√2×(1.5×10−2)3.51×1015
Calculating the above expression:
t=√3.0×10−23.51×1015≈√8.55×10−18≈2.93×10−9s
The time taken by the electron to fall a distance of 1.5 cm in the electric field is approximately:
t≈2.9×10−9s
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
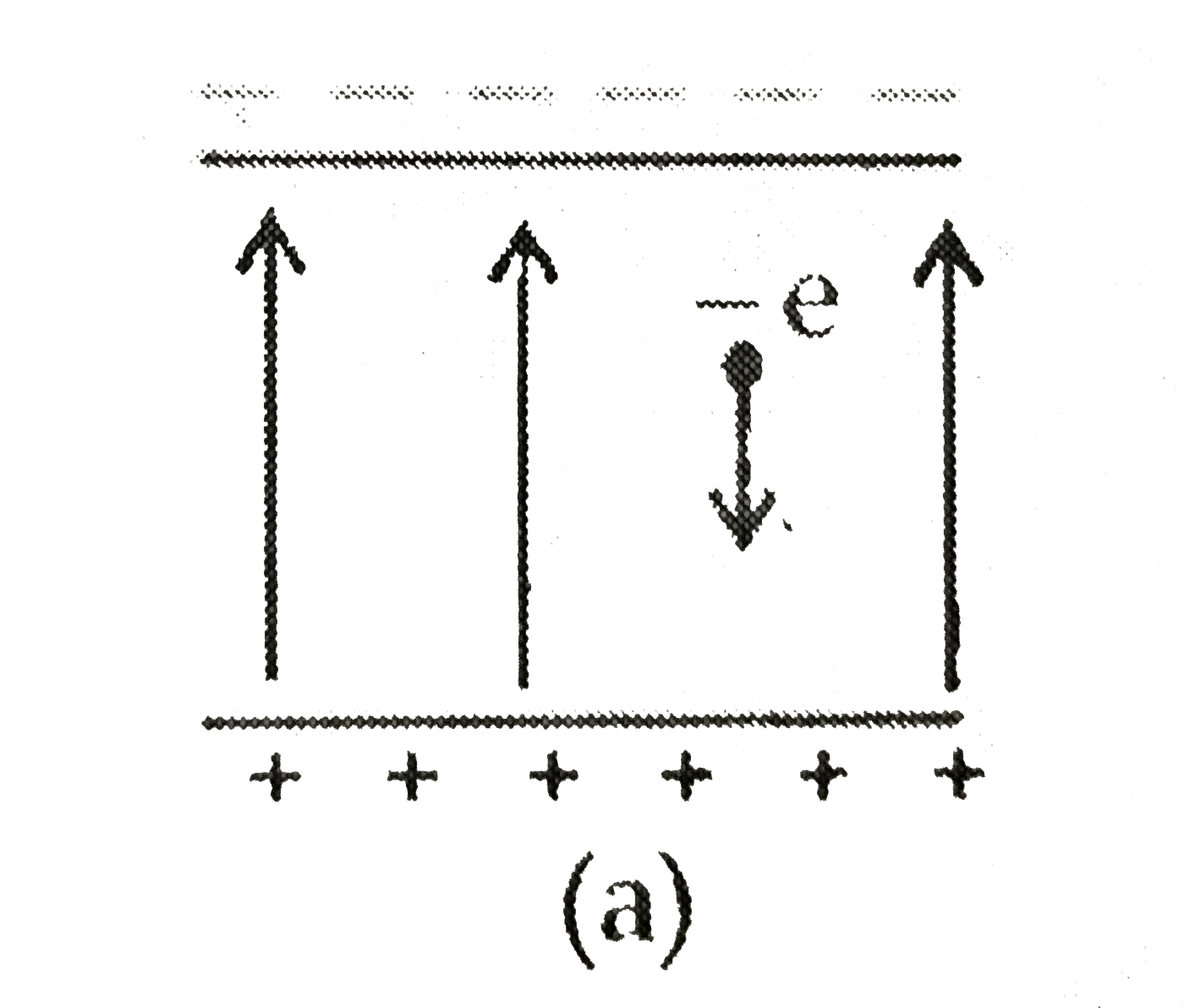
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
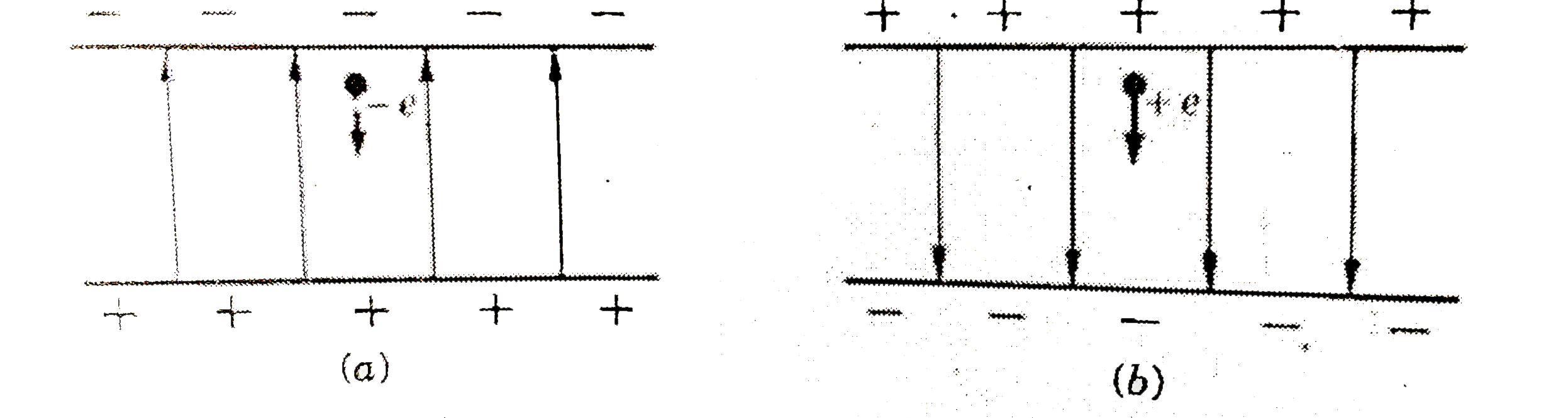
View Solution
Knowledge Check
An electron of mass Me, initially at rest, moves through a certain distance in a uniform electric field in time t1. A proton of mass Mp also initially at rest, takes time t2 to move through an equal distance in this uniform electric field. Neglecting the effect of gravity, the ratio t2/t1 is nearly equal to
A(mpme)1/2B(memp)1/2C1D1836
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
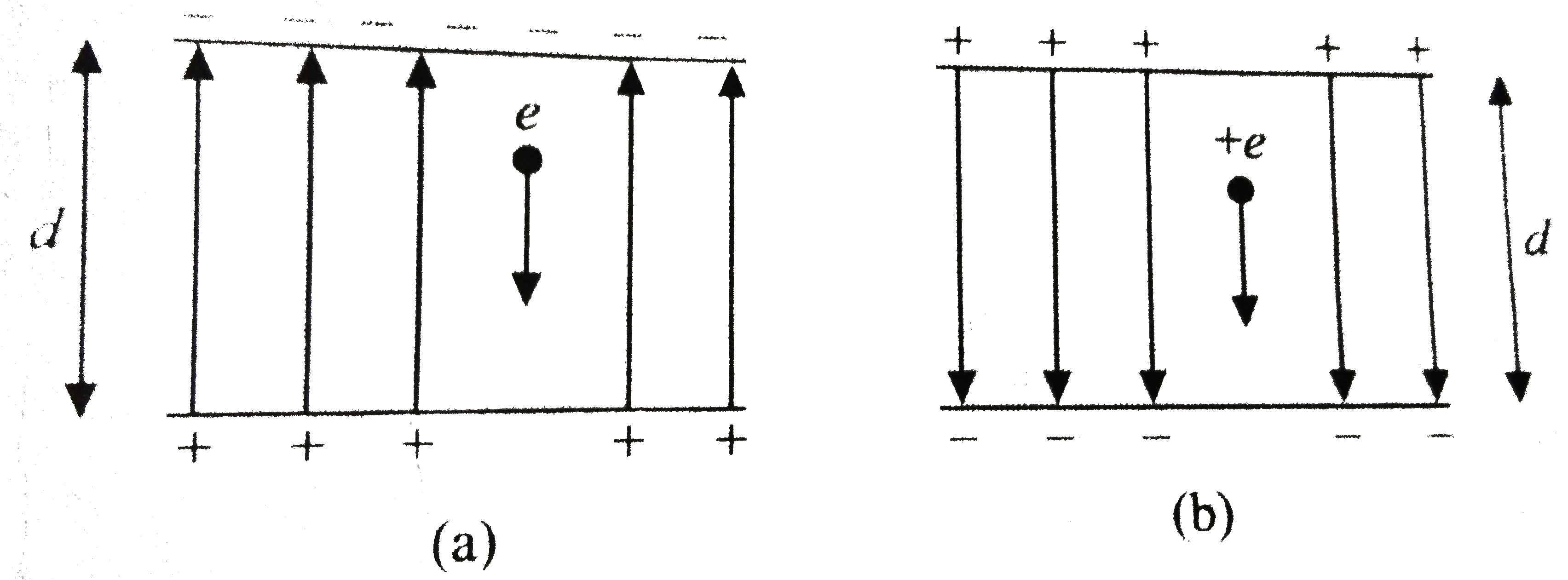 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAn electron (q=1.6×10−19C) is moving at right angles to a uniform magnetic field of 3.534×10−5 T The time taken by the electron to complete a circular orbit is
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View Solution
