An electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
1
√MpMe
√MeMp
1836
The correct Answer is:B
To solve the problem, we will analyze the motion of an electron and a proton in a uniform electric field and derive the relationship between the time taken by each particle to travel the same distance.
1. Understanding the Forces:
- The force acting on a charged particle in an electric field E is given by F=qE, where q is the charge of the particle.
- For an electron, q=−e (where e is the elementary charge), and for a proton, q=+e.
2. Calculating Acceleration:
- The acceleration a of a particle is given by Newton's second law F=ma.
- For the electron:
ae=Feme=qeEme=(−e)Eme
- For the proton:
ap=Fpmp=qpEmp=eEmp
3. Using the Equations of Motion:
- Both the electron and proton start from rest and travel the same distance d in times t1 and t2, respectively.
- The equation of motion for distance is:
d=ut+12at2
- Since both start from rest, u=0, so:
d=12aet21(for the electron)
d=12apt22(for the proton)
4. Setting the Distances Equal:
- Since both particles travel the same distance d:
12aet21=12apt22
- Canceling 12 gives:
aet21=apt22
5. Substituting the Accelerations:
- Substitute the expressions for ae and ap:
(−eEme)t21=(eEmp)t22
- Cancel eE (since both are positive and non-zero):
−t21me=t22mp
6. Rearranging for the Time Ratio:
- Rearranging gives:
t22t21=mpme
- Taking the square root:
t2t1=√mpme
Final Result:
The ratio of the time taken by the proton to the time taken by the electron is:
t2t1=√mpme
- The force acting on a charged particle in an electric field E is given by F=qE, where q is the charge of the particle.
- For an electron, q=−e (where e is the elementary charge), and for a proton, q=+e.
- The acceleration a of a particle is given by Newton's second law F=ma.
- For the electron:
ae=Feme=qeEme=(−e)Eme
- For the proton:
ap=Fpmp=qpEmp=eEmp
- Both the electron and proton start from rest and travel the same distance d in times t1 and t2, respectively.
- The equation of motion for distance is:
d=ut+12at2
- Since both start from rest, u=0, so:
d=12aet21(for the electron)
d=12apt22(for the proton)
- Since both particles travel the same distance d:
12aet21=12apt22
- Canceling 12 gives:
aet21=apt22
- Substitute the expressions for ae and ap:
(−eEme)t21=(eEmp)t22
- Cancel eE (since both are positive and non-zero):
−t21me=t22mp
- Rearranging gives:
t22t21=mpme
- Taking the square root:
t2t1=√mpme
The ratio of the time taken by the proton to the time taken by the electron is:
t2t1=√mpme
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View SolutionAn object of mass m, initially at rest under the action of a constant force F attains a velocity v in time t. Then, the average power supplied to mass is
View Solution
Knowledge Check
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.9×10−9s
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
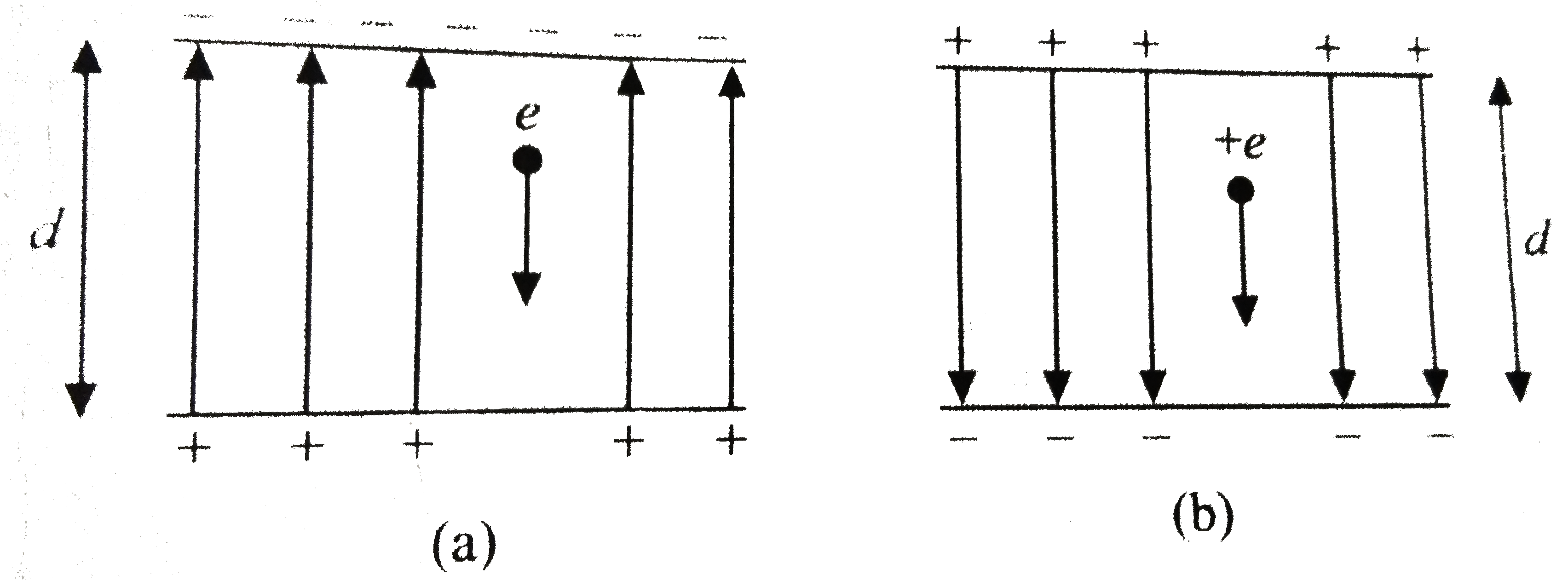 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionIn a region of uniform electric field ofn intencity E, an electron of mass me is released from rest. The distance travelled by the eloctron in a time t is
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron of mass m and charge e initially at rest gets accelerated by a constant electric field E. The rate of change of de-Broglie wavelength of this electron at time t ignoring relativistic effects is
View SolutionA proton and an α-particle start from rest in a uniform electric field, then the ratio of times of flight to travel same distance in the field is
View SolutionAn electron having charge 'e' and mass 'm' is moving a uniform electric field E. Its acceleration will be
View Solution
