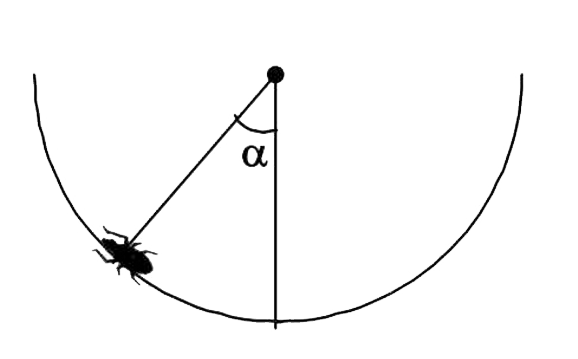
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
cotα=3
tanα=3
secα=3
cosecα=3
The correct Answer is:A
KEY CONCEPT:
For the maximum possible value of α,
mgsinα will also be maximum and equal to the frictional force.
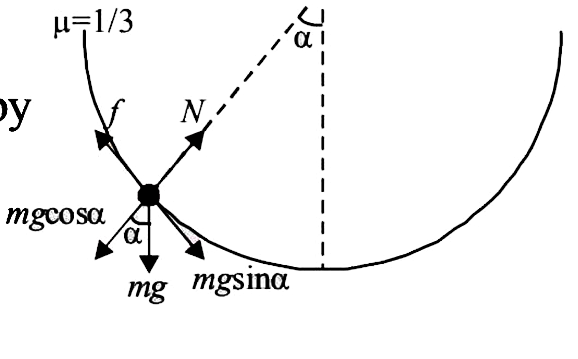
In this case f is the limiting friction. The two forces acting on the insect are mg and N. Let us resolve mg into two components. mgcosα balances N. mgsinα is balanced by the frictional force.
∴ N=mgcosα
f=mgsinα
But f=μN=μmgcosα
∴ μmgcosα=mgsinα⇒cotα=1μ⇒cotα=3
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Video
Similar Questions
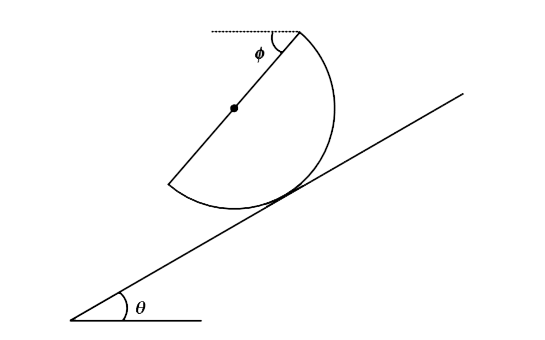
A uniform hemisphere placed on an incline is on verge of sliding. The coefficient of friction between the hemisphere and the incline is μ=0.3.
Find the angle ϕ that the circular base of the hemisphere makes with the horizontal.
Given sin(tan−10.3)≅0.29 and sin−1(0.77)≅50∘
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View Solution
Knowledge Check
An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1]The coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
A0.4mB0.2mC0.3mD0.1m
A rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple O either at the very beginning or not at all just before coming to rest only if the coefficient of friction at the ground O is > 1 only if some external force acts on it in addition to the frictional force
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be .
View Solution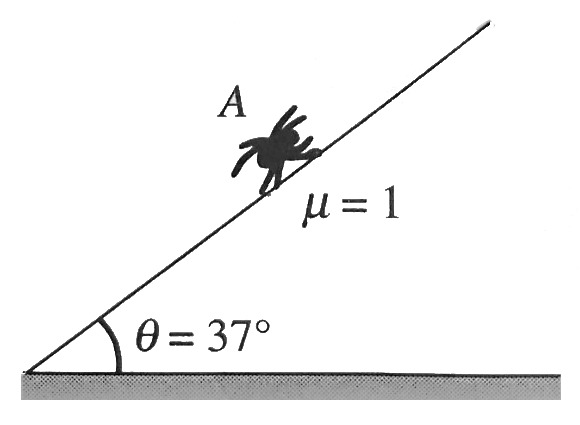
An insect of mass m, starts moving on a rough inclined surface from point A. As the surface is vert sticky, the corfficient of fricion between the insect and the incline is μ=1. Assume that it can move in any direction, up the incline or down the incline then
View SolutionA particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View Solution
A solid sphere of mass m and radius R is rolling without slipping on a rough horizontal surface with angular acceleration α. Centre of mass of sphere lies at a distance R√2 from the centre of sphere. Find the normal force applied by sphere on the surface at an instant when line joining centre of mass of sphere and centre of sphere makes an angle 45∘ with the vertical and angular velocity of sphere at this instant is ω.
View Solution
