An object is taken from a point P to another point Q in a gravitational field:
assuming the earth to be spherical, if both P and Q lie on the earth's surface, the work done is zero
if P is on the earth's surface and Q above it, the work done is minimum when it is taken along the straight line PQ
the work done depends only on the position of P and Q and is independent of the path along which the particle is taken
there is no work done if the object is taken from P to Q and then brought back to P along any path
The correct Answer is:A, C, D
To solve the problem, we need to analyze the work done when an object is moved in a gravitational field from point P to point Q. We will evaluate the given options one by one.
1. Understanding Work Done in a Gravitational Field:
Work done (W) in a gravitational field is defined as the force applied (F) multiplied by the displacement (d) in the direction of the force. Mathematically, W = F * d * cos(θ), where θ is the angle between the force and the displacement.
2. Option 1: Both P and Q lie on Earth's Surface:
If both points P and Q are on the Earth's surface, they are at the same height from the center of the Earth. Since gravitational potential energy depends on height, and there is no change in height when moving horizontally on the surface, the work done is 0.
- Conclusion: Option 1 is true.
3. Option 2: P on Earth's Surface and Q Above It:
If point P is on the Earth's surface and point Q is above it, the work done will depend on the height difference between P and Q. The minimum work done will occur when the object is moved directly upward along the straight line from P to Q, as this minimizes the distance traveled against the gravitational force.
- Conclusion: This option is misleading because while the work done is indeed minimized along the straight line, it does not imply that the work done depends on the path taken. The work done is determined solely by the change in gravitational potential energy, which depends on the height difference.
4. Option 3: Work Done Depends Only on Position:
The work done in moving an object in a gravitational field is independent of the path taken and depends only on the initial and final positions. This is a fundamental principle in conservative forces like gravity.
- Conclusion: Option 3 is true.
5. Option 4: No Work Done if Object is Returned to P:
If the object is moved from P to Q and then back to P along any path, the initial and final positions are the same. Therefore, the net work done over the entire journey is 0, as the work done in moving to Q is equal and opposite to the work done in returning to P.
- Conclusion: Option 4 is true.
Final Answer:
The true statements regarding the work done when moving an object in a gravitational field are:
- Option 1: True
- Option 3: True
- Option 4: True
Work done (W) in a gravitational field is defined as the force applied (F) multiplied by the displacement (d) in the direction of the force. Mathematically, W = F * d * cos(θ), where θ is the angle between the force and the displacement.
If both points P and Q are on the Earth's surface, they are at the same height from the center of the Earth. Since gravitational potential energy depends on height, and there is no change in height when moving horizontally on the surface, the work done is 0.
- Conclusion: Option 1 is true.
If point P is on the Earth's surface and point Q is above it, the work done will depend on the height difference between P and Q. The minimum work done will occur when the object is moved directly upward along the straight line from P to Q, as this minimizes the distance traveled against the gravitational force.
- Conclusion: This option is misleading because while the work done is indeed minimized along the straight line, it does not imply that the work done depends on the path taken. The work done is determined solely by the change in gravitational potential energy, which depends on the height difference.
The work done in moving an object in a gravitational field is independent of the path taken and depends only on the initial and final positions. This is a fundamental principle in conservative forces like gravity.
- Conclusion: Option 3 is true.
If the object is moved from P to Q and then back to P along any path, the initial and final positions are the same. Therefore, the net work done over the entire journey is 0, as the work done in moving to Q is equal and opposite to the work done in returning to P.
- Conclusion: Option 4 is true.
The true statements regarding the work done when moving an object in a gravitational field are:
- Option 1: True
- Option 3: True
- Option 4: True
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension
23 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Single Correct
122 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
A point charge is taken from a point A to a pint B in an electric field. Does the work done by the electric field depend on the path of the charge ?
View SolutionTwo particles of masses 'm' and '9m' are separated by a distance 'r'. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is (G = Universal constant of gravitation)
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionAn aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.
View SolutionIf a unit positive charge is taken from one point to another over an equipotential surface ,then
View SolutionGravitational potential at a distance 'r' from a point mass 'm' is
V=−GMr
Find gravitational field strength at that point.
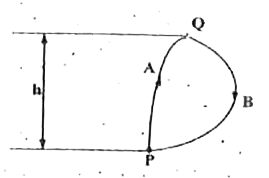
View SolutionA particle is taken from point P to point Q via the path PAQ and then placed back to point P via the path QBP. Find the work done by gravity on the body over this closed path. Vertical separation between P and Q is h as shown.
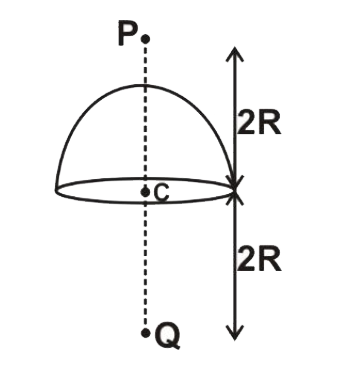
View SolutionIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
View SolutionGravitational potential difference between a point on surface of planet and another point 10 m above is 4J/kg. Considering gravitational field to be uniform, how much work is donw in moving a mass of 2kg from the surface to a point 5 m above the surface?
View SolutionAssertion : If gravitational potential at some point is zero, then gravitational field strength at that point will also be zero.
Reason : Except at infinity gravitational potential due to a system of point masses at some finite distance can't be zero.
View Solution
