AN oscillating block-spring system has a mechanical energy of 2.00J, an amplitude of 10.0cm, and a maximum speed of 0.800 m/s. Find (a) the spring constant, (b) the mass of the block and (c ) the frequency of oscillation.
To solve the problem step by step, we will find the spring constant (k), the mass of the block (m), and the frequency of oscillation (f) based on the given data.
Given Data:
- Mechanical Energy (E) = 2.00 J
- Amplitude (A) = 10.0 cm = 0.1 m
- Maximum Speed (V_max) = 0.800 m/s
Step 1: Finding the Spring Constant (k)
The mechanical energy of a block-spring system in simple harmonic motion is given by the formula:
E=12kA2
Where:
- E is the mechanical energy,
- k is the spring constant,
- A is the amplitude.
Substituting the given values into the equation:
2.00=12k(0.1)2
2.00=12k(0.01)
2.00=0.005k
Now, solve for k:
k=2.000.005=400N/m
Step 2: Finding the Mass of the Block (m)
The maximum speed in simple harmonic motion is given by:
Vmax=Aω
Where:
- ω is the angular frequency.
Rearranging the equation to find ω:
ω=VmaxA
Substituting the known values:
ω=0.8000.1=8rad/s
Now, we know that the angular frequency is also related to the spring constant and mass by:
ω=√km
Squaring both sides gives:
ω2=km
Rearranging to find m:
m=kω2
Substituting the values of k and ω:
m=40082=40064=6.25kg
Step 3: Finding the Frequency of Oscillation (f)
The frequency of oscillation is related to the angular frequency by:
f=ω2π
Substituting the value of ω:
f=82π=4π≈1.27Hz
Final Answers:
(a) Spring constant, k=400N/m
(b) Mass of the block, m=6.25kg
(c) Frequency of oscillation, f≈1.27Hz
- Mechanical Energy (E) = 2.00 J
- Amplitude (A) = 10.0 cm = 0.1 m
- Maximum Speed (V_max) = 0.800 m/s
E=12kA2
Where:
- E is the mechanical energy,
- k is the spring constant,
- A is the amplitude.
2.00=12k(0.1)2
2.00=12k(0.01)
2.00=0.005k
Now, solve for k:
k=2.000.005=400N/m
Vmax=Aω
Where:
- ω is the angular frequency.
ω=VmaxA
Substituting the known values:
ω=0.8000.1=8rad/s
ω=√km
Squaring both sides gives:
ω2=km
Rearranging to find m:
m=kω2
Substituting the values of k and ω:
m=40082=40064=6.25kg
f=ω2π
Substituting the value of ω:
f=82π=4π≈1.27Hz
(a) Spring constant, k=400N/m
(b) Mass of the block, m=6.25kg
(c) Frequency of oscillation, f≈1.27Hz
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
An oscillating mass spring system has mechanical energy 1 joule, when it has an amplitude 0.1 m and maximum speed of 1ms−1. Then the force constant of the spring is
A100 Nm−1B200 Nm−1C300 Nm−1D50 Nm−1 - Question 2 - Select One
An oscillating mass spring system has mechanical energy 1 joule, when it has an amplitude 0.1m and maximum speed of 1ms−1. The force constant of the spring is (in Nm−1)
A100B200C300D50 - Question 3 - Select One
In the figure all spring are identical having spring constant k and mass m each .The block hav also mass m .The frequency of oscillation of the block is
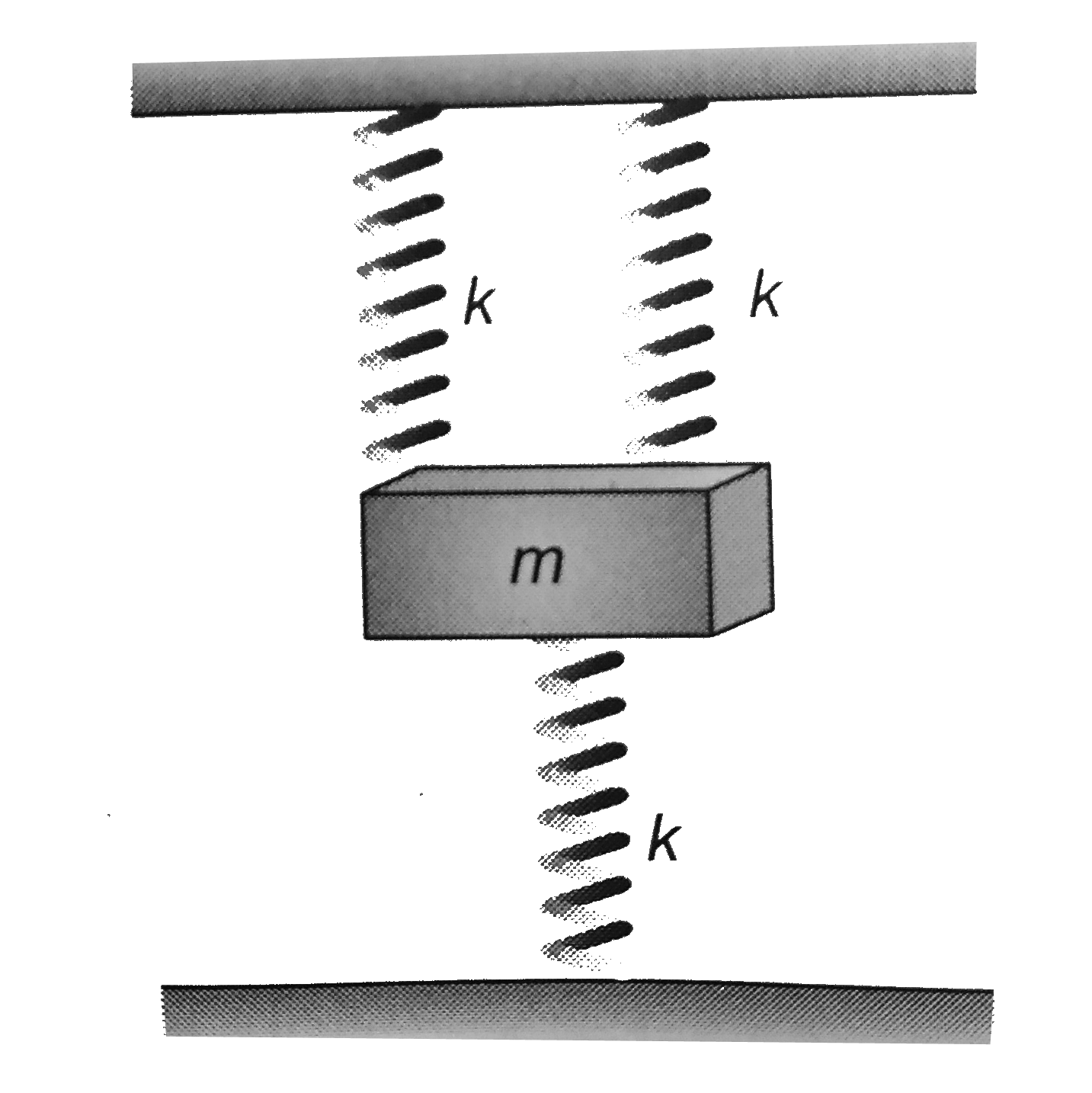 A12π√3kmB12π√3k2mC2π√3m3kDNone of these
A12π√3kmB12π√3k2mC2π√3m3kDNone of these
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314s. Find the maximum fore exerted by the spring on the blockl.
View SolutionAn object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 View Solution
View SolutionA block weighing 10.0 N is attached to the lower end of a verticle spring (k=200.0N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
What is the amplitude of the oscillation and the maximum kinetic energy of the block as it oscillates?View Solution


