An oscillator consists of a block attached to a spring (k= 425N/m). At some time t, the position (measured from the system's equilibrium location), velocity and acceleration of the block are x= 0.100m, v=13.6m/s,anda=−123m/s2. Calculate (a) the frequency of oscillation, (b) the mass of the block and (c ) the amplitude of the motion.
(a) 5.58Hz, (b) 0.346kg, (c ) 0.401m
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
A simple harmonic oscillator consists of a block attached to a spring with k=200N/m. The block slides on a frictionless horizontal surface, with equilibrium point x=0. A graph of the block velocity v as a function of time t is shown. Correct match the required information in the left column with the values given in table.
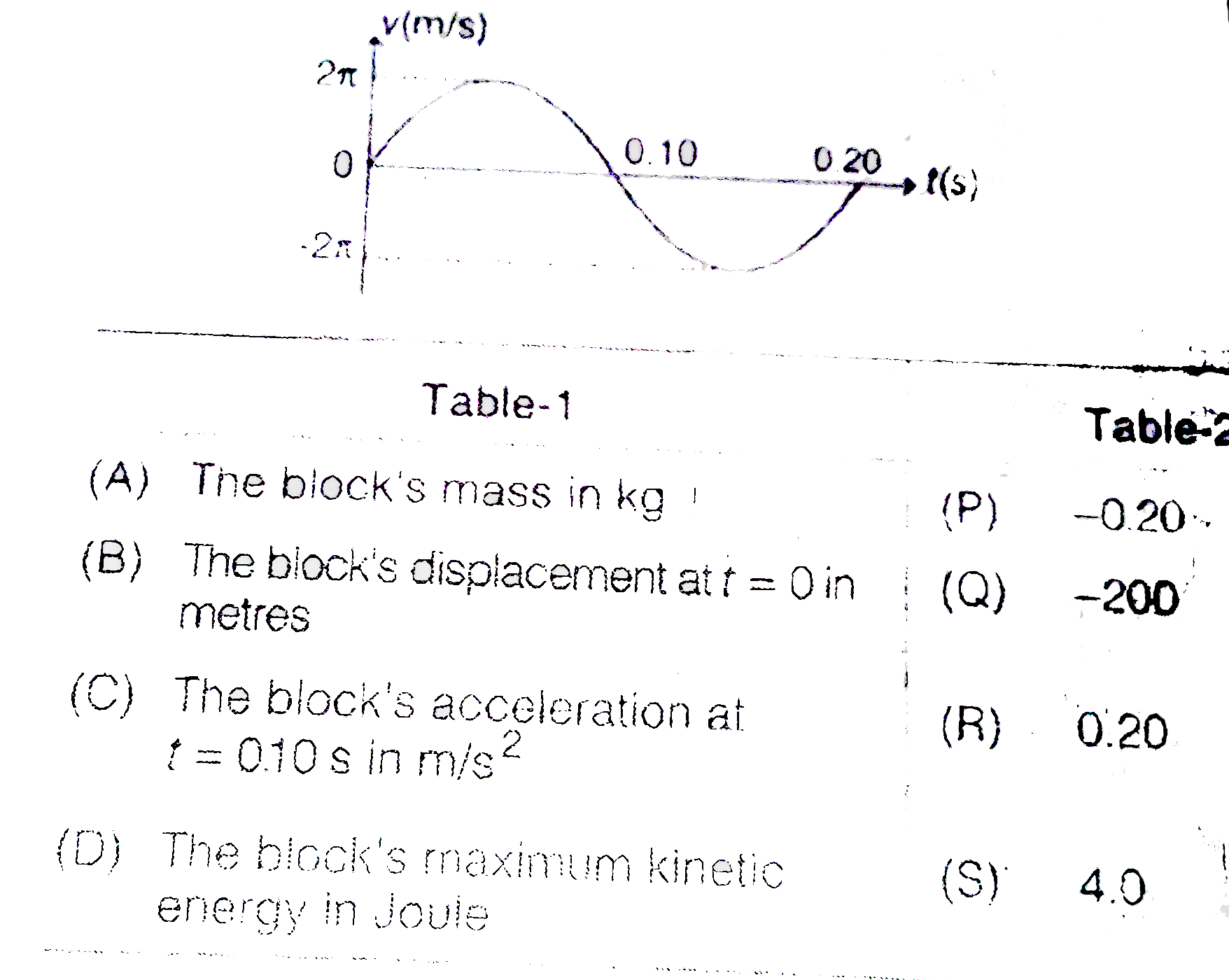 View Solution
View SolutionAN oscillating block-spring system has a mechanical energy of 2.00J, an amplitude of 10.0cm, and a maximum speed of 0.800 m/s. Find (a) the spring constant, (b) the mass of the block and (c ) the frequency of oscillation.
View Solution
Knowledge Check
- Question 1 - Select One
An oscillator consists of a block attached to a spring of spring constant K=300 N/m. At some time t the position (measured from its equilibrium position), velocity and acceleration of the block are
x=0.1m,v=−15m/s and a=−90m/s2. What is the ampliof motion and the mass of the block ?A0.3 m and 0.3 kgB0.4 m and 14kgC0.5 and 13kgD0.5m and 14kg - Question 2 - Select One
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
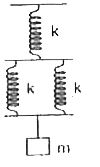 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km - Question 3 - Select One
An elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A spring-block system is executing SHM. The mass of the block is M and the time period of oscillation is T. If the mass of the block is increased by m, then time period becomes 7T4. Now, find the ratio of mM ,
View Solution
A block of mass m is connected to a spring of spring constant k as shown in Fig. The block is found at its equilibrium position t=1s and it has a velocity of +0.25ms at t=2s. The time period of oscillation is 6 s. Based on the given information answer the following question: Q. the amplitude of oscillation isView SolutionA block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 View Solution
View SolutionFor a damped oscillator the mass 'm' of the block is 200 g, k = 90 N m−1 and the damping constant b is 40 g s−1. Calculate the period of oscillation.
View SolutionIf acceleration of block B is 4m/s2 upward & that of C is 6m/s2 downward. Find acceleration of A :−
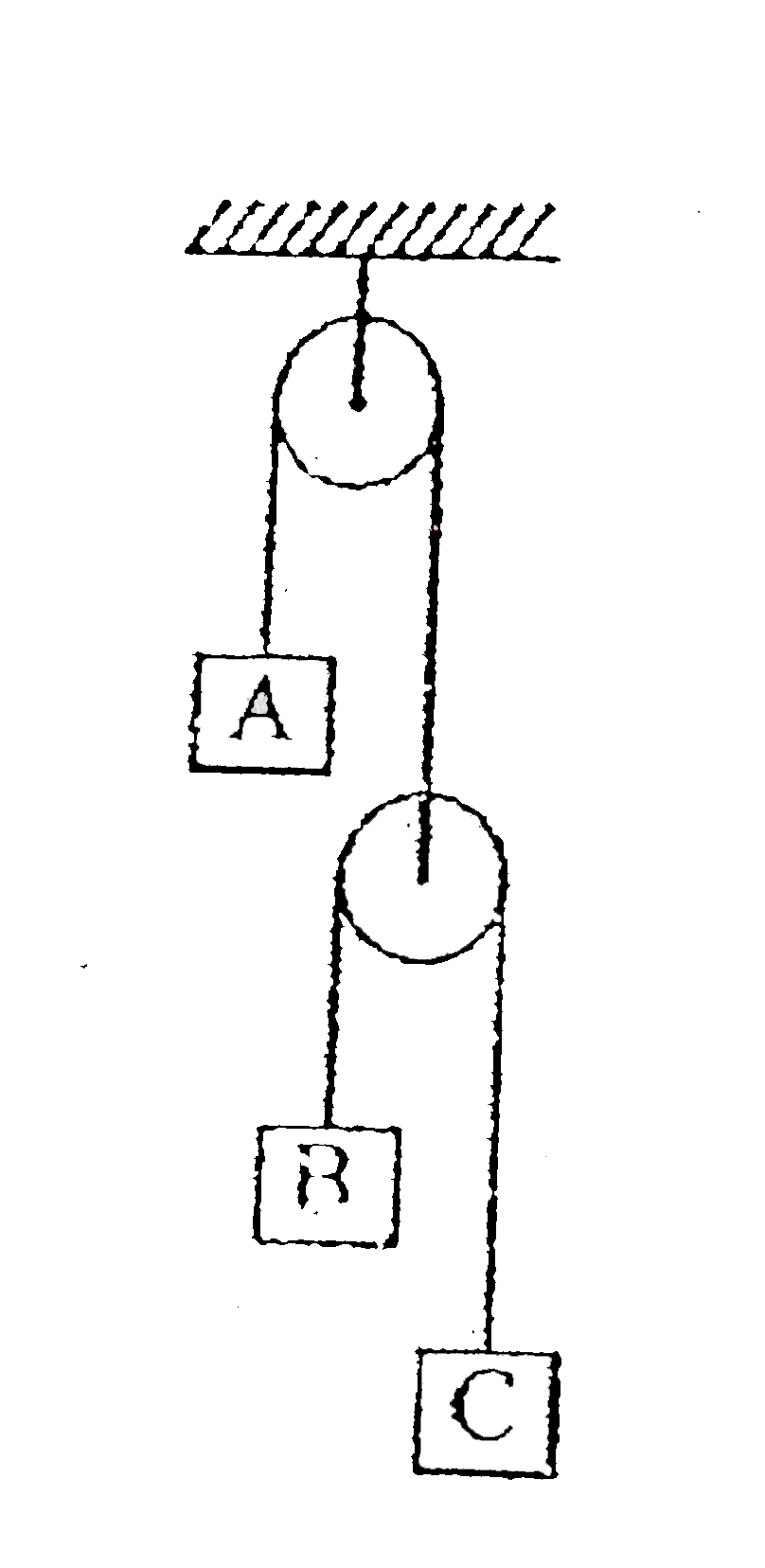 View Solution
View Solution

