Assertion: Every wire is like a spring, whose spring constant ,K∝1l, where l is length of wire.
Reason : It follows from the relation
K=YAl
(a) If both Assertion and Reason are true and the Reason is correctn explanation of the Assertion.
(b) If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A
To solve the problem, we need to analyze the assertion and the reason provided in the question step by step.
Step 1: Understanding the Assertion
The assertion states that every wire behaves like a spring, and its spring constant K is inversely proportional to its length l. This means that as the length of the wire increases, the spring constant decreases.
Step 2: Understanding the Reason
The reason provided is based on the formula for the spring constant K given by:
K=YAl
where:
- Y is the Young's modulus of the material,
- A is the cross-sectional area of the wire,
- l is the length of the wire.
Step 3: Analyzing the Formula
From the formula K=YAl, we can see that:
- K is directly proportional to the Young's modulus Y and the cross-sectional area A,
- K is inversely proportional to the length l.
This implies that if the length l increases, the spring constant K decreases, confirming the assertion.
Step 4: Conclusion
Since both the assertion and the reason are true, and the reason correctly explains the assertion, we conclude that:
- The assertion is true.
- The reason is true and provides the correct explanation for the assertion.
Final Answer
Both the assertion and the reason are true, and the reason is the correct explanation of the assertion.
---
The assertion states that every wire behaves like a spring, and its spring constant K is inversely proportional to its length l. This means that as the length of the wire increases, the spring constant decreases.
The reason provided is based on the formula for the spring constant K given by:
K=YAl
where:
- Y is the Young's modulus of the material,
- A is the cross-sectional area of the wire,
- l is the length of the wire.
From the formula K=YAl, we can see that:
- K is directly proportional to the Young's modulus Y and the cross-sectional area A,
- K is inversely proportional to the length l.
Since both the assertion and the reason are true, and the reason correctly explains the assertion, we conclude that:
- The assertion is true.
- The reason is true and provides the correct explanation for the assertion.
Both the assertion and the reason are true, and the reason is the correct explanation of the assertion.
Topper's Solved these Questions
- ELASTICITYBook:DC PANDEY ENGLISHChapter:ELASTICITYExercise:Level 1 Single Correct
Explore 16 Videos
- ELASTICITYBook:DC PANDEY ENGLISHChapter:ELASTICITYExercise:Level 1 Subjective
Explore 8 Videos
- ELASTICITYBook:DC PANDEY ENGLISHChapter:ELASTICITYExercise:Exercise 15.2
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 469 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Integer
Explore 17 Videos
Similar Questions
Which of the following graph depicts spring constant k versus length l of the spring correctly
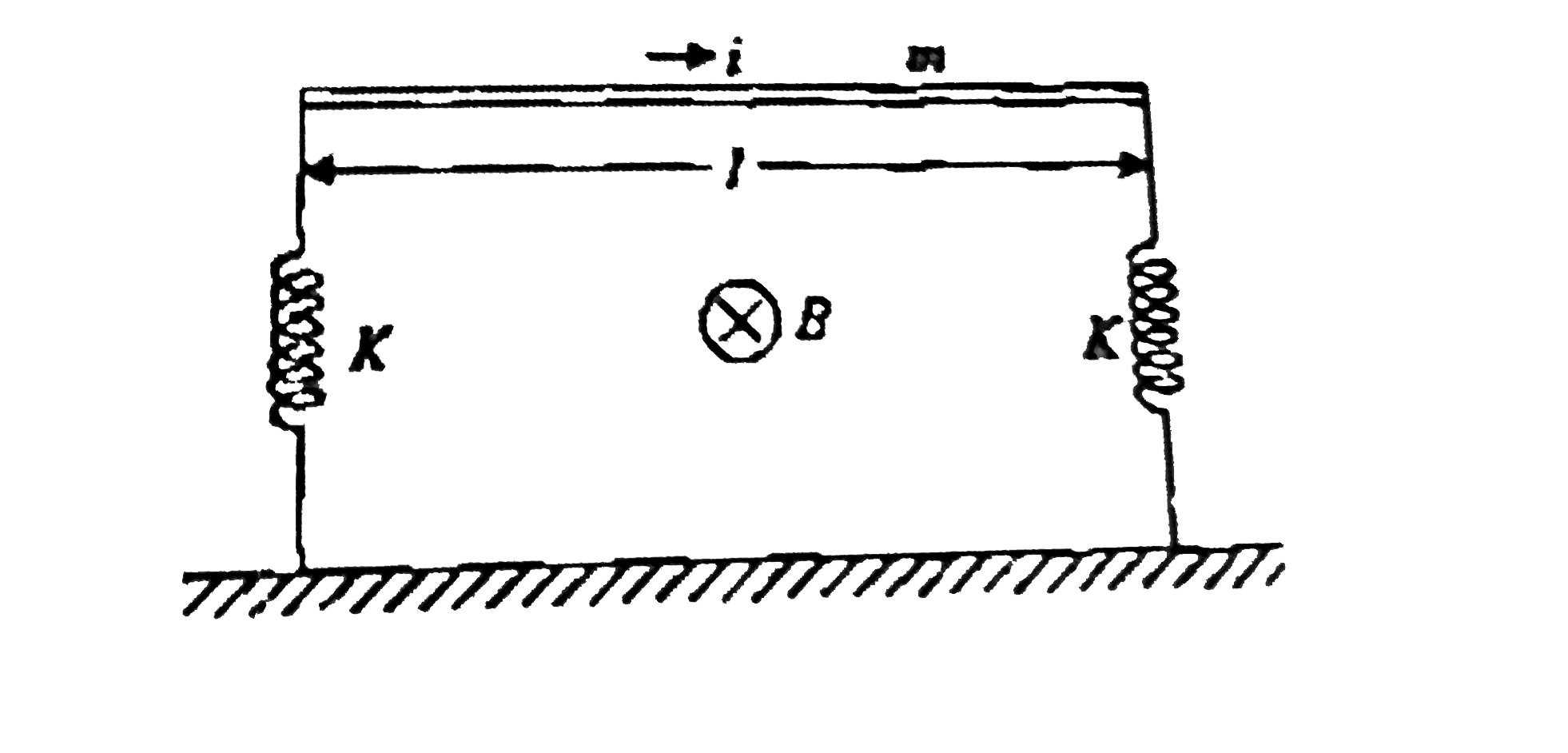
View SolutionA horizontal metallic rod of mass 'm' and length 'l' is supported by two vertical identical springs of spring constant 'k' each and natral length l0 A current 'l' is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be

View SolutionWhen heat is supplied to the gas it expands and displaces piston by L/2 where natural length of springs are L = 1 m. Spring constant K = 100 N/m. Area of piston is 1m2. The pressure of gas in final situation is

View SolutionThe string is now replaced by a spring of spring constant k and natural length l. Mass 2m is fixed at the bottom of the frame . The mass m which has the other end of the spring attached to it is brought near the mass 2m and released as shown in figure. The maximum angle θ that the spring will substend at the centre will be :( Take k=10N/m,l=1m,m=1kg and l=r)

View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution