Assertion : Peak value of current in AC through a resistance of 10Ω is 2A. Then, power consumed by the resistance should be 20W.
Reason : Power in AC is P=I2rmsR
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A, B
P=I2rmsR
=(2√2)2(10)
=20W
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Objective30videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 28.22videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
Find the current through 2Ω and 4Ω resistance.
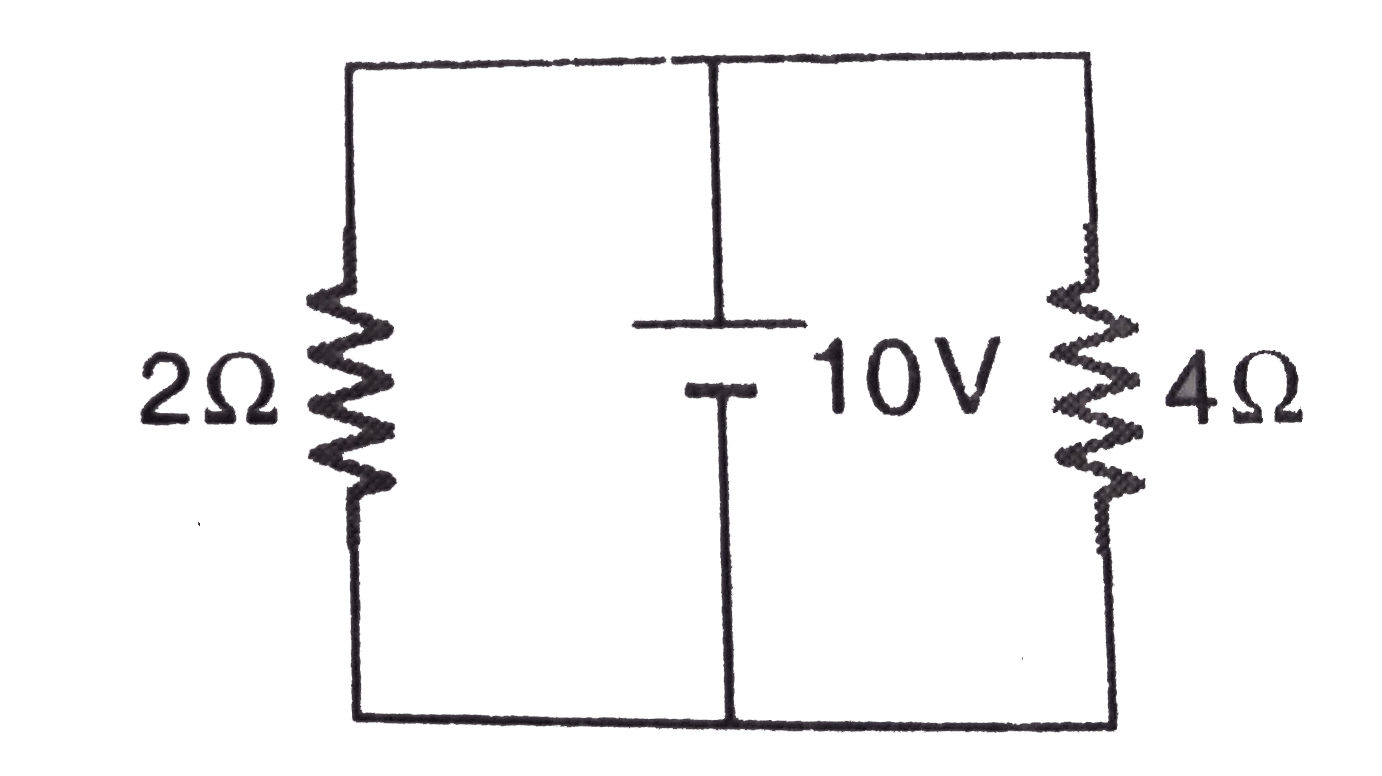 View Solution
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionIn the circuit shown, current through the resistance2Ω isi1 and current through the resistance30Ω is i2. The ratio i1i2 is equal to
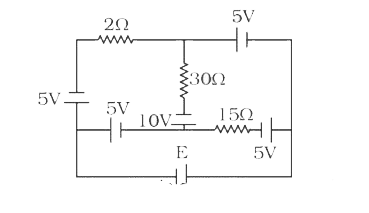 View Solution
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionIf the cell of emf 5 volt shown in the figure gives a power of 10W. Q, find the powers consumed by the resistors 2Ω and 1Ω
 View Solution
View SolutionIf the cell of emf 5 volt shown in the figure gives a power of 10W. Q, find the powers consumed by the resistors 2Ω and 1Ω
 View Solution
View Solution110Vrms is applied across a series circuit having resistance 11Ω and impedance 22Ω . The power consumed is
View SolutionStatement I: When an external resistor of resistance R (connected across a cell to internal resistance r ) is varied, power consumed by resistance R is maximum when R = r.
Statement II: Power consumed by a resistor of constant resistance R is maximum when current through it is maximum.View Solution

