Calculate the electrostatic potential energy for a system of three point charges q placed at the corners of an equilateral triangle of side ‘a’.
To calculate the electrostatic potential energy for a system of three point charges q placed at the corners of an equilateral triangle of side a, we can follow these steps:
Step 1: Identify the charges and their positions
We have three point charges, each of charge q, located at the corners of an equilateral triangle. Let's denote the charges as Q1=q, Q2=q, and Q3=q.
Step 2: Calculate the potential energy between each pair of charges
The electrostatic potential energy U between two point charges Q1 and Q2 separated by a distance r is given by the formula:
U=14πϵ0Q1Q2r
In our case, the distance r between any two charges is equal to the side length a of the triangle.
Step 3: Calculate the potential energy for each pair
We need to calculate the potential energy for the three pairs of charges:
1. Between Q1 and Q2:
U12=14πϵ0q⋅qa=q24πϵ0a
2. Between Q2 and Q3:
U23=14πϵ0q⋅qa=q24πϵ0a
3. Between Q1 and Q3:
U13=14πϵ0q⋅qa=q24πϵ0a
Step 4: Sum the potential energies
The total electrostatic potential energy U of the system is the sum of the potential energies of all pairs:
U=U12+U23+U13
Substituting the values we calculated:
U=q24πϵ0a+q24πϵ0a+q24πϵ0a
U=3⋅q24πϵ0a
Step 5: Final expression for the potential energy
Thus, the total electrostatic potential energy for the system of three point charges is:
U=3q24πϵ0a
We have three point charges, each of charge q, located at the corners of an equilateral triangle. Let's denote the charges as Q1=q, Q2=q, and Q3=q.
The electrostatic potential energy U between two point charges Q1 and Q2 separated by a distance r is given by the formula:
U=14πϵ0Q1Q2r
In our case, the distance r between any two charges is equal to the side length a of the triangle.
We need to calculate the potential energy for the three pairs of charges:
1. Between Q1 and Q2:
U12=14πϵ0q⋅qa=q24πϵ0a
U23=14πϵ0q⋅qa=q24πϵ0a
U13=14πϵ0q⋅qa=q24πϵ0a
The total electrostatic potential energy U of the system is the sum of the potential energies of all pairs:
U=U12+U23+U13
Substituting the values we calculated:
U=q24πϵ0a+q24πϵ0a+q24πϵ0a
U=3⋅q24πϵ0a
Thus, the total electrostatic potential energy for the system of three point charges is:
U=3q24πϵ0a
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS
6 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS
49 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (2 MARKS)
59 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
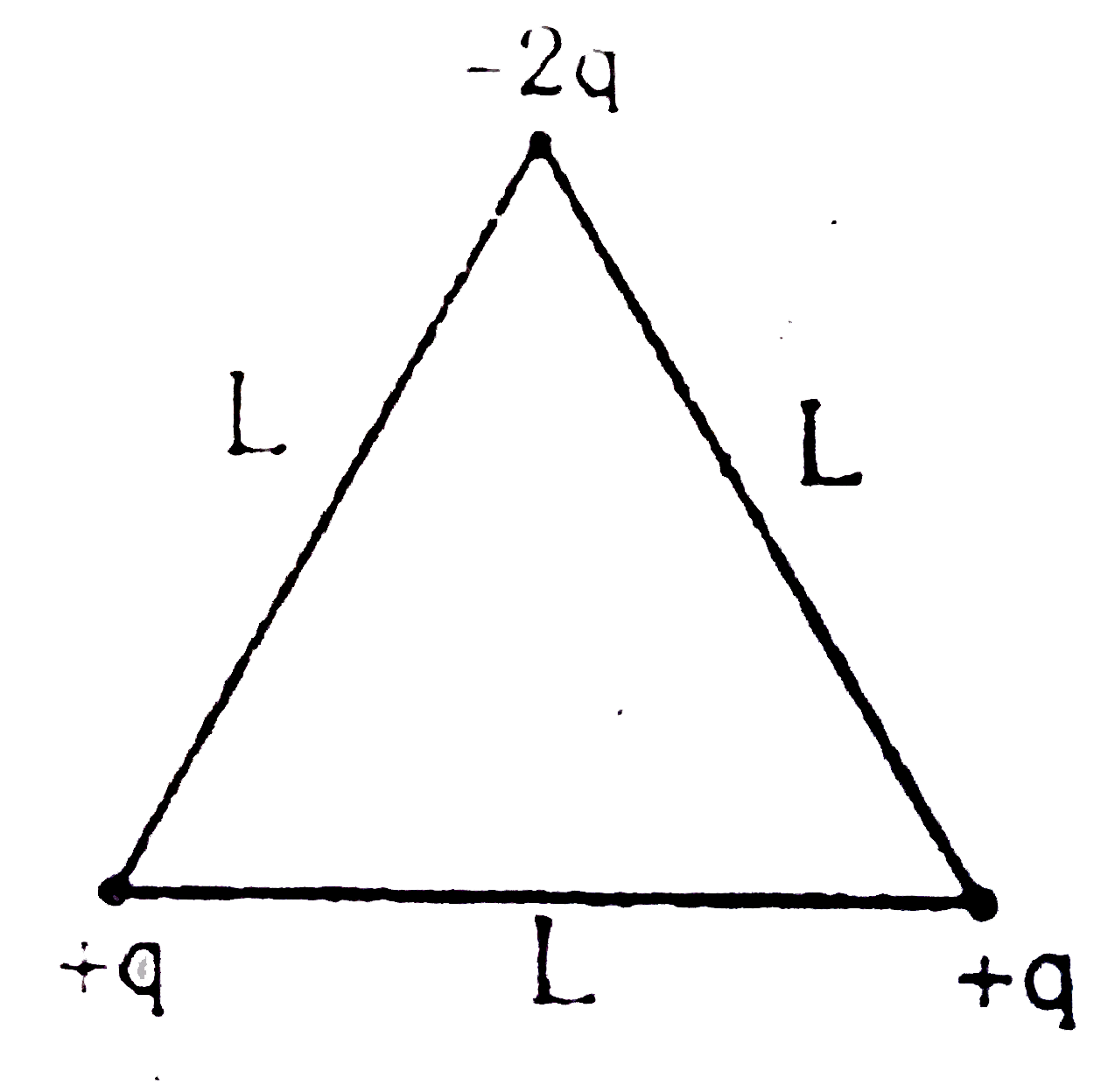
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
View SolutionCalculate the electrostatic potential energy of a system of three point charges q1,q2 and q3 located respectively at →r1,→r2 and →r3 with respect to a common origin O.
View Solution
Knowledge Check
Three point charges are placed at the corner of an equilateral triangle. Assuming only electrostatic forces are acting.
Athe system can never be in equilibriumBthe system will be equilibrium if the charges rotate about the centre of the triangleCthe system will be in equilibrium if the charges have different magnitudes and different signsDthe system will be in equilibrium if the charges have the same magnitude but different signs.The gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
A−Gm2xB−Gm23xC−3Gm2xD3Gm2x2The gravitational potential energy of an isolated system of three particles, each of mass m, at the three corners of an equilateral triangle of side l is
A−Gm2lB−Gm22lC−2Gm2lD−3Gm2l
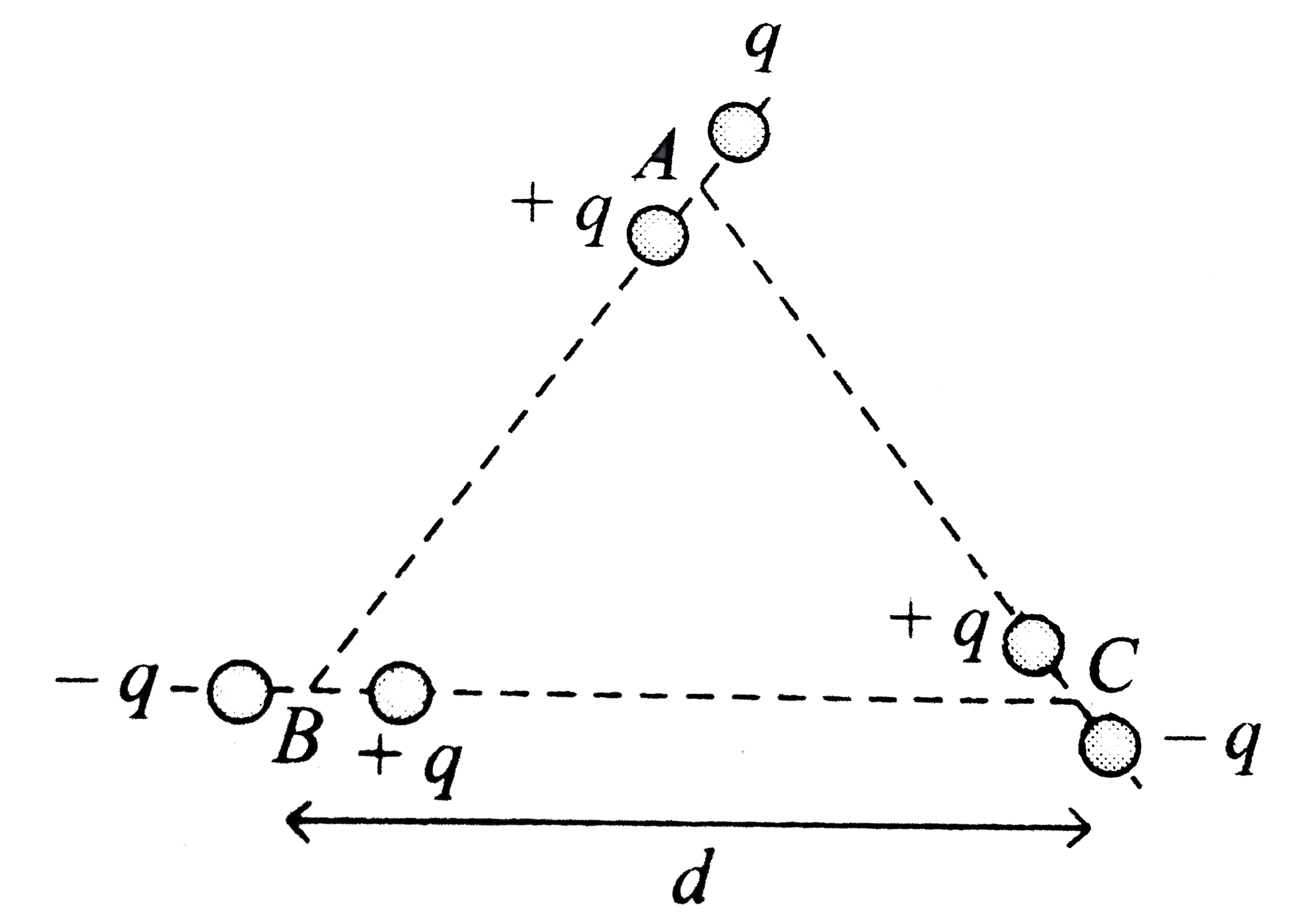
Three identical dipoles with charges q and −q, and separation A between the charges, are placed at the corners of an equilateral triangle of side D as shown in fig. Find the interaction energy of the system (a<<d).
 .
.
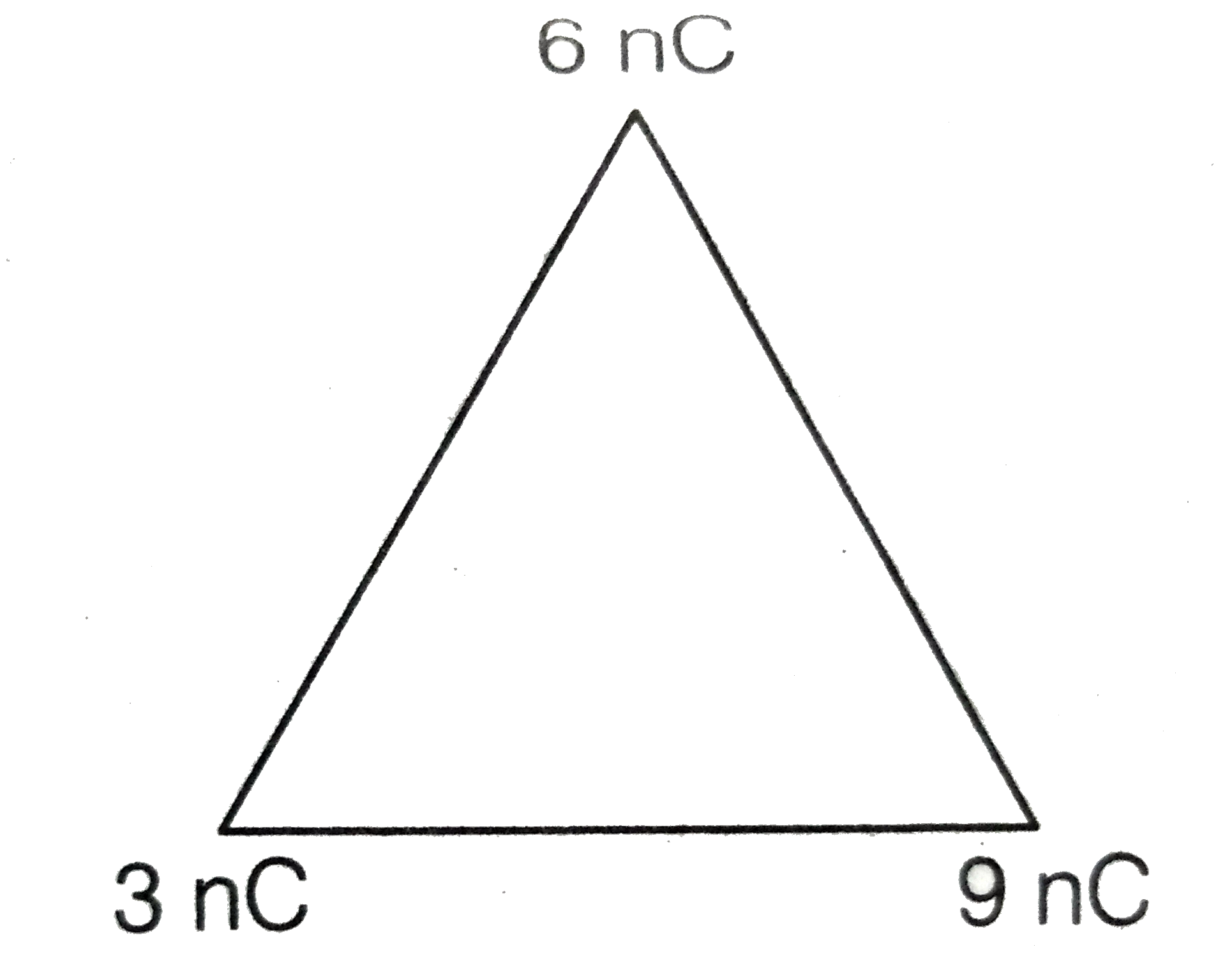
View SolutionThree point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
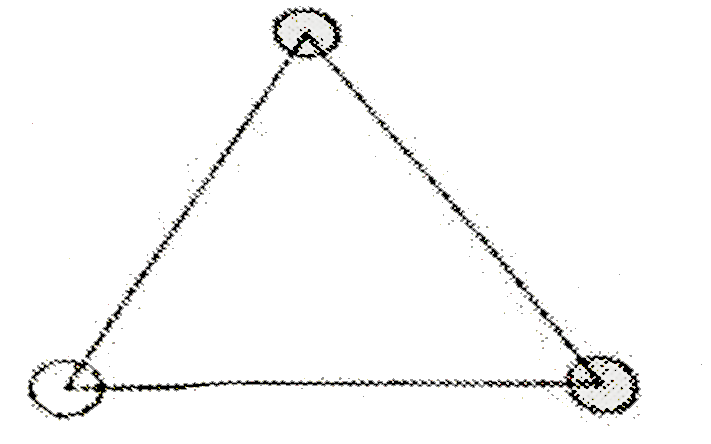
View SolutionThree small conducting spheres each of radius a and charge q is placed at the corners of an equilateral triangle of side lenth /. The side lenth / is considerably larger than dimensions of the spheres. Find the electrical potential energy of system.
View SolutionThree charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View Solution
