Conisder a thin spherical shell of radius R with centre at the origin, carrying uniform poistive surface charge denisty. The variation of the magnitude of the electric field ∣∣→E(r)∣∣ and the electric potential V(r) with the distance r from the centre, is best represented by which graph?
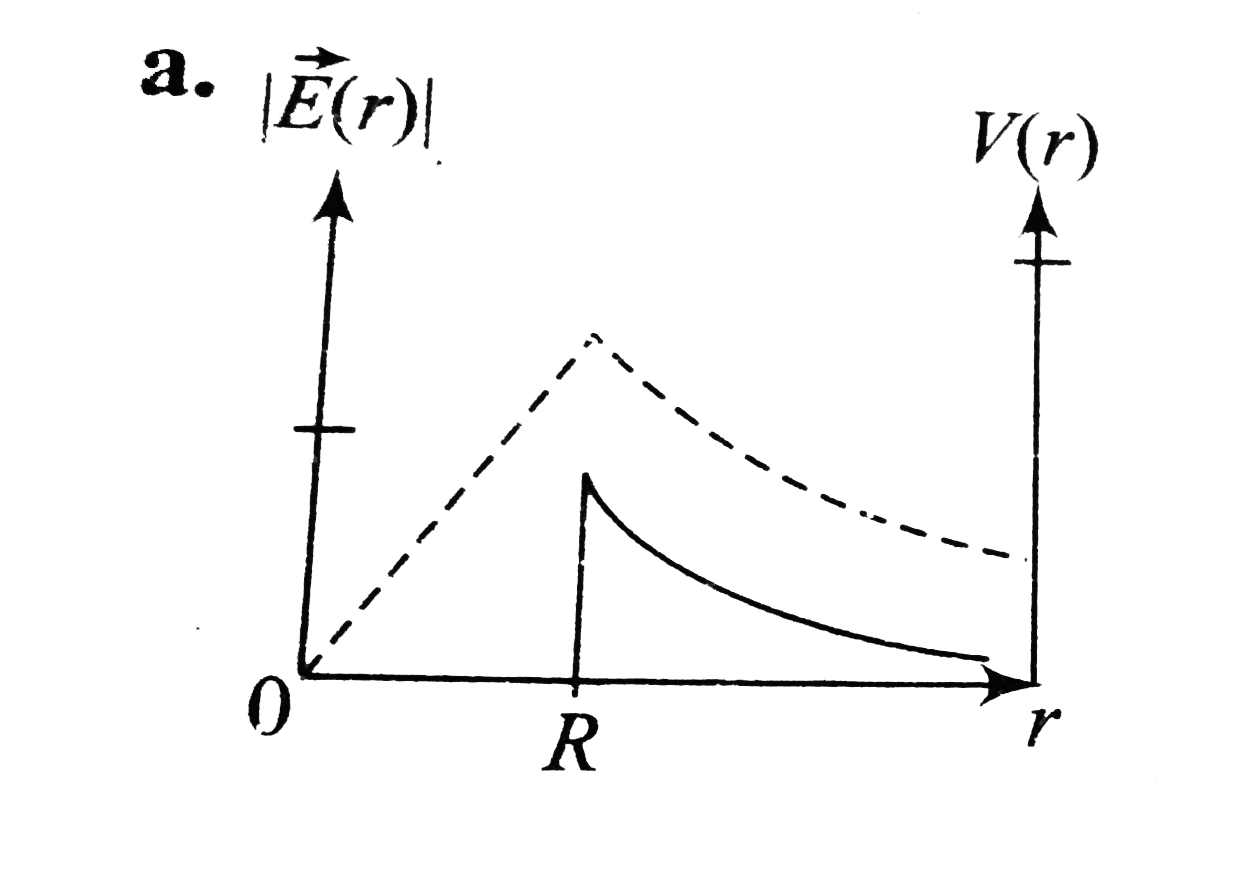
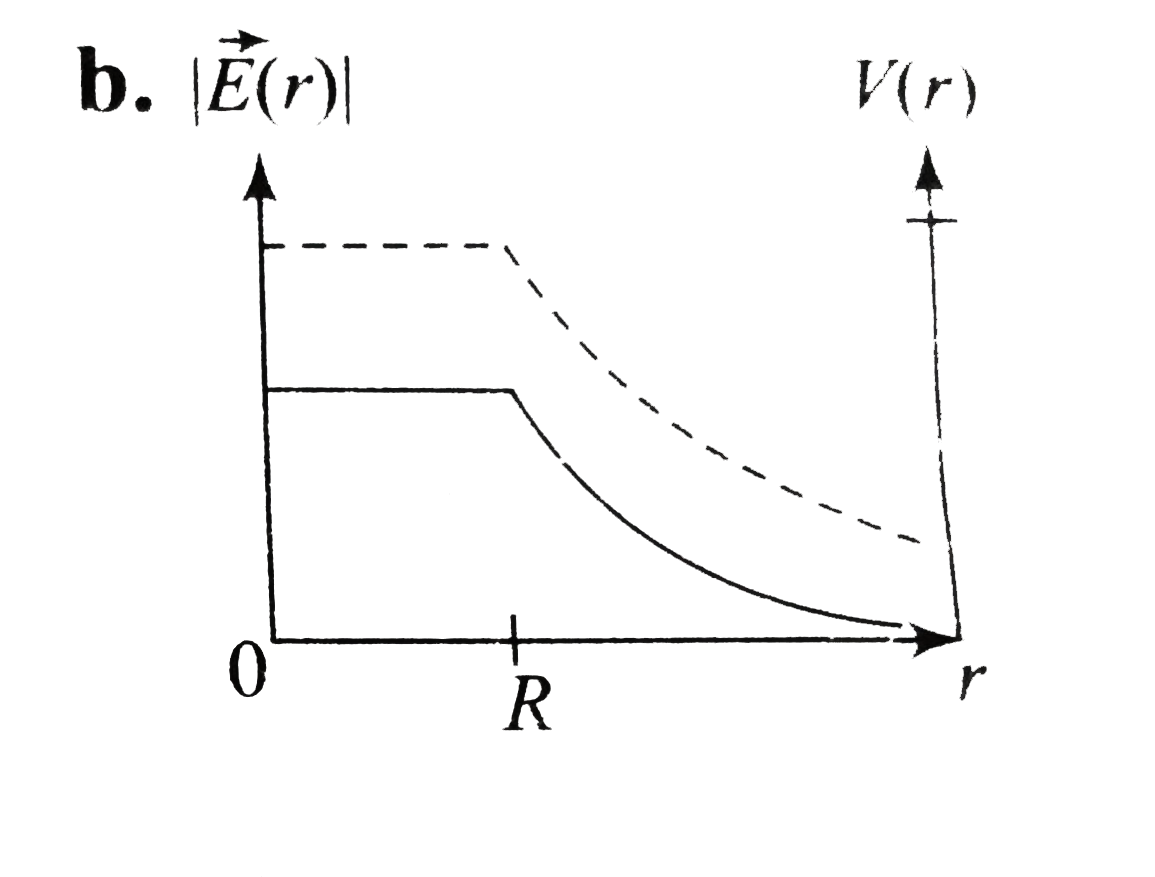
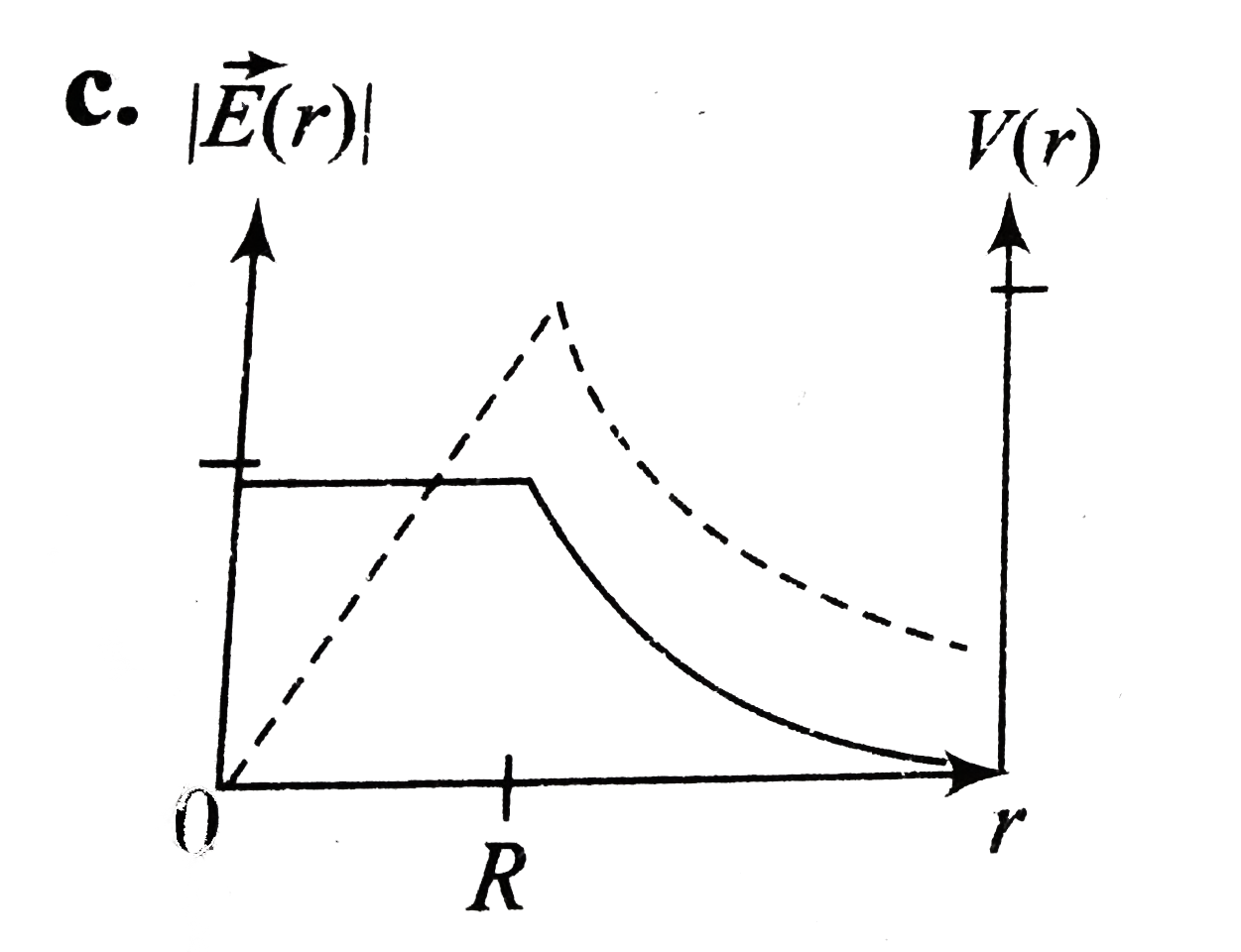
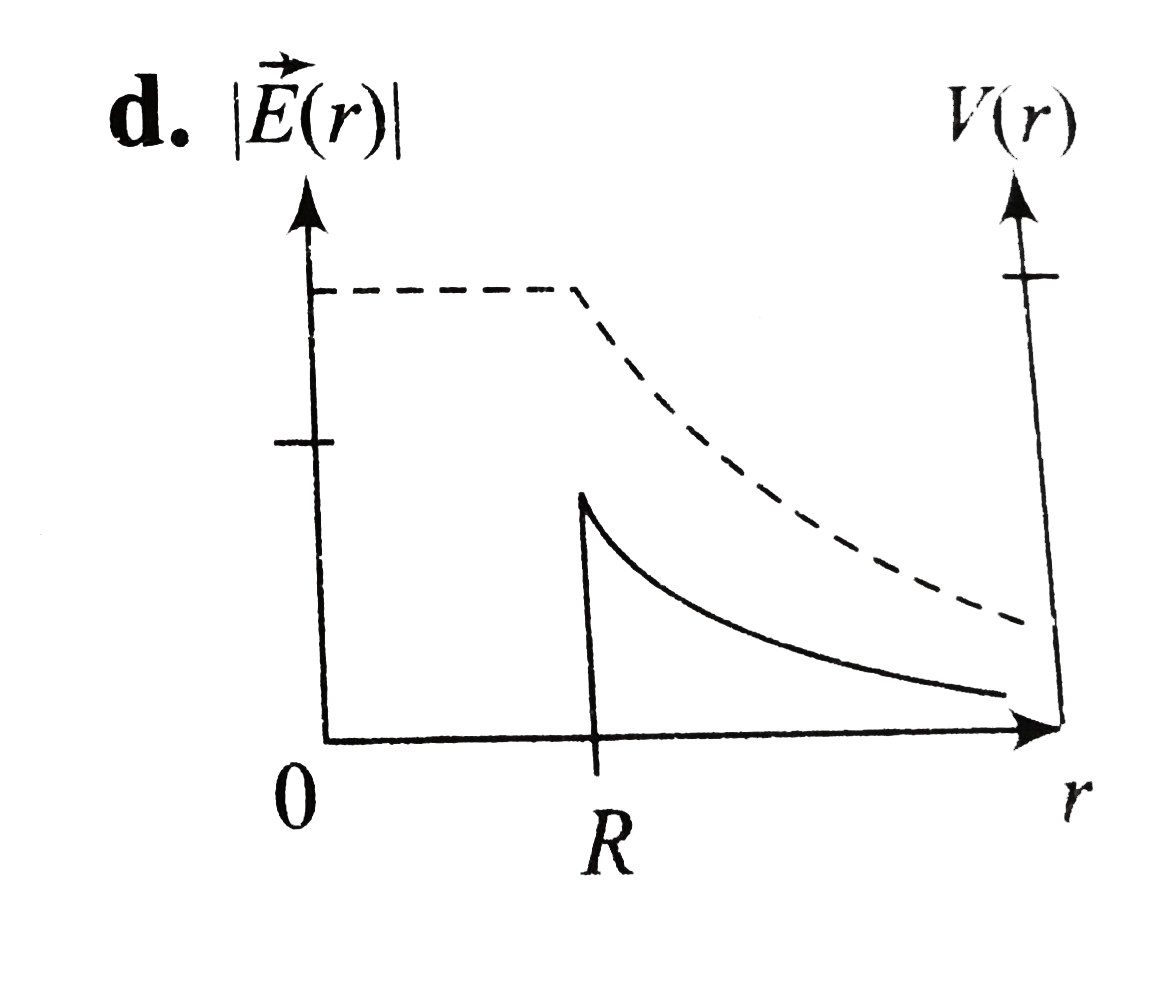
To solve the problem regarding the electric field and electric potential due to a thin spherical shell with uniform positive surface charge density, we will analyze the behavior of both quantities at different distances from the center of the shell.
1. Understanding the System:
We have a thin spherical shell of radius R with a uniform positive surface charge density. We need to analyze the electric field |→E(r)| and the electric potential V(r) at various distances r from the center of the shell.
2. Electric Field Inside the Shell:
According to Gauss's law, the electric field inside a uniformly charged spherical shell is zero. Therefore, for r<R:
|→E(r)|=0
3. Electric Field on the Surface of the Shell:
At the surface of the shell (where r=R), the electric field can be calculated using the formula:
|→E(R)|=KQR2
where K is Coulomb's constant and Q is the total charge on the shell.
4. Electric Field Outside the Shell:
For points outside the shell (where r>R), the electric field behaves as if all the charge were concentrated at the center:
|→E(r)|=KQr2
5. Graphing Electric Field:
- For r<R: |→E(r)|=0
- For r=R: |→E(R)|=KQR2 (maximum value)
- For r>R: |→E(r)| decreases as 1r2
The graph of the electric field will be zero for r<R, a maximum at r=R, and will decrease inversely with the square of r for r>R.
6. Electric Potential Inside the Shell:
The electric potential inside the shell (for r<R) is constant and equal to the potential at the surface:
V(r)=V(R)=KQR
7. Electric Potential on the Surface of the Shell:
At the surface, the potential is:
V(R)=KQR
8. Electric Potential Outside the Shell:
For r>R, the potential decreases as:
V(r)=KQr
9. Graphing Electric Potential:
- For r<R: V(r)=KQR (constant)
- For r=R: V(R)=KQR
- For r>R: V(r) decreases as 1r
The graph of the electric potential will be a horizontal line for r<R, and then it will decrease as 1r for r>R.
Conclusion
The variation of the electric field and electric potential with distance r from the center of the shell is best represented by the graphs where:
- The electric field is zero inside the shell, reaches a maximum at the surface, and decreases as 1r2 outside.
- The electric potential is constant inside the shell and decreases as 1r outside.
We have a thin spherical shell of radius R with a uniform positive surface charge density. We need to analyze the electric field |→E(r)| and the electric potential V(r) at various distances r from the center of the shell.
According to Gauss's law, the electric field inside a uniformly charged spherical shell is zero. Therefore, for r<R:
|→E(r)|=0
At the surface of the shell (where r=R), the electric field can be calculated using the formula:
|→E(R)|=KQR2
where K is Coulomb's constant and Q is the total charge on the shell.
For points outside the shell (where r>R), the electric field behaves as if all the charge were concentrated at the center:
|→E(r)|=KQr2
- For r<R: |→E(r)|=0
- For r=R: |→E(R)|=KQR2 (maximum value)
- For r>R: |→E(r)| decreases as 1r2
The electric potential inside the shell (for r<R) is constant and equal to the potential at the surface:
V(r)=V(R)=KQR
At the surface, the potential is:
V(R)=KQR
For r>R, the potential decreases as:
V(r)=KQr
- For r<R: V(r)=KQR (constant)
- For r=R: V(R)=KQR
- For r>R: V(r) decreases as 1r
The variation of the electric field and electric potential with distance r from the center of the shell is best represented by the graphs where:
- The electric field is zero inside the shell, reaches a maximum at the surface, and decreases as 1r2 outside.
- The electric potential is constant inside the shell and decreases as 1r outside.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
 View Solution
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View Solution
Knowledge Check
- Question 1 - Select One
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
Variation of electric potential due to npn-conducting (positively charged) solid sphere with distance from its centre is best represented as
View SolutionA thin spherical shell of radius R has charge Q spread uniformly over its surface. Which of the following graphs most closely represents the electric field E(r) produced by the shell in the range 0≤r<∞, where r is the distance from the centre of the shell?
View SolutionA thin spherical shell of radius R has charge Q spread uniformly over its surface. Which of the following graphs most closely represents the electric field E(r) produced by the shell in the range 0≤r<∞, where r is the distance from the centre of the shell?
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionThe electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?
View Solution
