Consider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistance but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity (ω) in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it.
Find the magnitude of this force when the rod makes an angle (θ) with the vertical.
B2a3ω2R−mgsinθ
B2a3ω2R+mgsinθ
B2a3ωR−mgsinθ
None of these
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the rod and the induced electromotive force (EMF) due to its rotation in a magnetic field. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Rod
The rod has a weight mg acting downwards. When the rod makes an angle θ with the vertical, the weight can be resolved into two components:
- The component acting along the direction of the rod: mgcosθ
- The component acting perpendicular to the rod: mgsinθ
Step 2: Determine the Induced EMF
As the rod rotates in a magnetic field, an electromotive force (EMF) is induced in it. The formula for the induced EMF E when a rod of length A rotates with angular velocity ω in a magnetic field B is given by:
E=12BωA2
Step 3: Calculate the Current
The current I flowing through the circuit can be calculated using Ohm's law:
I=ER=12BωA2R=BωA22R
Step 4: Calculate the Magnetic Force
The magnetic force FB acting on the rod due to the current in the magnetic field is given by:
FB=I⋅B⋅L=(BωA22R)⋅B⋅A=B2ωA32R
Step 5: Set Up the Force Balance
To maintain a constant angular velocity, the net force acting on the rod must be zero. The magnetic force FB acts in one direction, while the component of the weight mgsinθ acts in the opposite direction. Thus, we can write the force balance as:
FB−mgsinθ=0
This implies:
FB=mgsinθ
Step 6: Substitute for FB
Substituting the expression for FB into the force balance equation gives:
B2ωA32R=mgsinθ
Step 7: Solve for the Force F
Now, we can express the force F that needs to be applied at the midpoint of the rod to maintain the rotation:
F=mgsinθ−B2ωA32R
Final Answer
Thus, the magnitude of the force F required to maintain the uniform angular velocity ω when the rod makes an angle θ with the vertical is:
F=mgsinθ−B2ωA32R
The rod has a weight mg acting downwards. When the rod makes an angle θ with the vertical, the weight can be resolved into two components:
- The component acting along the direction of the rod: mgcosθ
- The component acting perpendicular to the rod: mgsinθ
As the rod rotates in a magnetic field, an electromotive force (EMF) is induced in it. The formula for the induced EMF E when a rod of length A rotates with angular velocity ω in a magnetic field B is given by:
E=12BωA2
The current I flowing through the circuit can be calculated using Ohm's law:
I=ER=12BωA2R=BωA22R
The magnetic force FB acting on the rod due to the current in the magnetic field is given by:
FB=I⋅B⋅L=(BωA22R)⋅B⋅A=B2ωA32R
To maintain a constant angular velocity, the net force acting on the rod must be zero. The magnetic force FB acts in one direction, while the component of the weight mgsinθ acts in the opposite direction. Thus, we can write the force balance as:
FB−mgsinθ=0
This implies:
FB=mgsinθ
Substituting the expression for FB into the force balance equation gives:
B2ωA32R=mgsinθ
Now, we can express the force F that needs to be applied at the midpoint of the rod to maintain the rotation:
F=mgsinθ−B2ωA32R
Thus, the magnitude of the force F required to maintain the uniform angular velocity ω when the rod makes an angle θ with the vertical is:
F=mgsinθ−B2ωA32R
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
View SolutionConsider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when <AOC=90∘.
View SolutionIf the rod were translating as well as rotating, what will be its emf? Assume that the centre of mass has a velocity v and the rod is rotating with an angular velocity ω atout its centre of mass.
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA rod of length l and total charge 'q' which is uniformly distributed is rotating with angular velocity ω about an axis passing through the centre of rod and perpendicular to rod. Find the magnitude of magnetic dipole moment (in Amp. m2) of rod. If q=4C,ω=3rad/s and l=2m
View SolutionShows a conducting circular loop radius a placed in a uniform, perpendicular magnetic field B. A metal rod OA is pivoted at the centre O of the loop. The other A of the rod touches the loop. The rod OA and the loop are resistanceless but a resistor having a resistance R is connected between O and a fixed point C on the loop . the rod OA is made to rotate anticlockwise at a small but uniform angular speed omega by an external force. Find (a) the current in the resistance R and (b) the torque of the external force needed ot keep the rod rotating with the constant angular velocity omega.
 View Solution
View SolutionFigure shows a situation similar to the previous problem. All parameters are the same except that a battery of emf ε and a variable resistance R are connected between O and C. The connecting wires have zero resistance. No external force is applied on the rod (except gravity, forces by the magnetic field and by the pivot).

In what way should the resistance R be changed so that the rod may rotate with uniform angular velocity in the clockwise direction? Express your answer in terms of the given quantities and the angle (θ) made by the rod OA with the horizontal.View SolutionA conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of VB−VA is
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
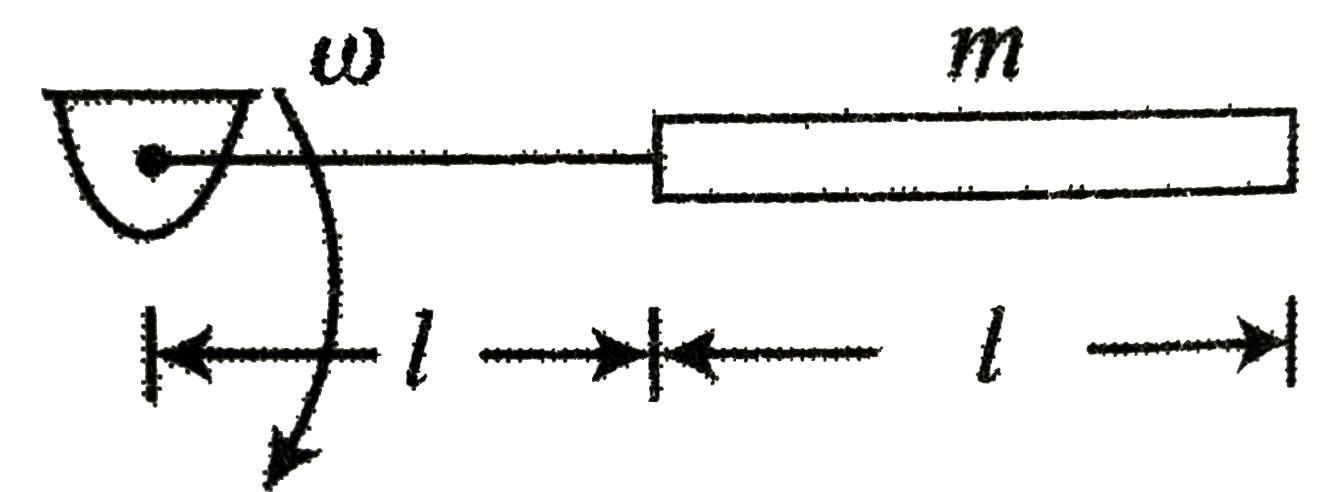
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.View Solution

