Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
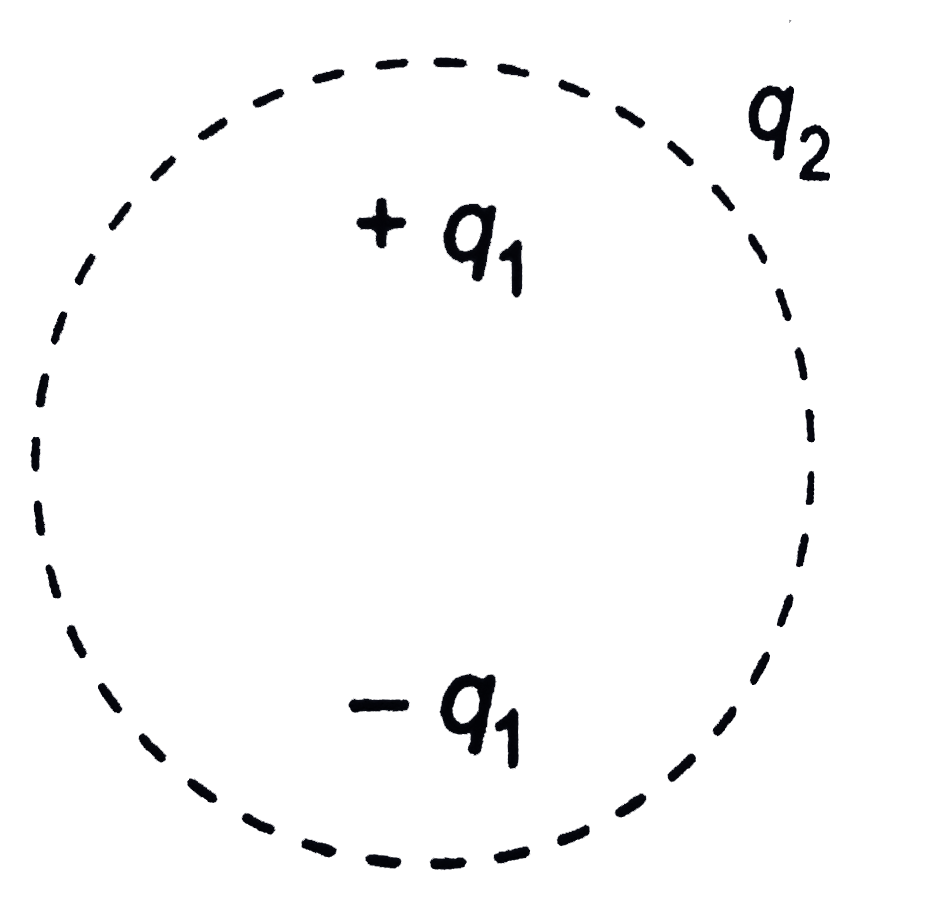
alone
and
and
and
The correct Answer is:C
Step by step video & image solution for Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns5videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
If the flux of the electric field through a closed surface is zero,
View SolutionA Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be
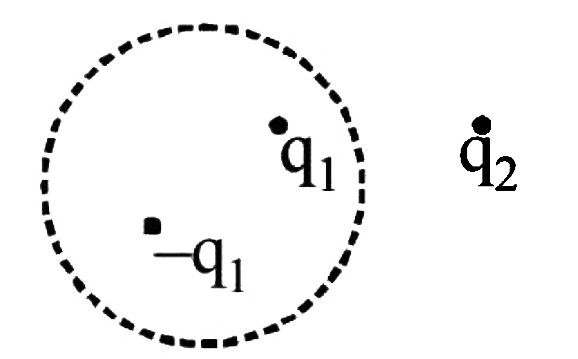
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionElectric flux through a spherical surface shown in the figure is
_______View SolutionFind the flux due to the electric field through the curved surface (R is radius of curvature)
View SolutionA small metal sphere carrying charge +Q is located at the centre of a spherical cavity inside a large uncharged metallic spherical shell as shown in the figure. Use Gauss’s law to find the expressions for the electric field at points p1 and p2 . Also draw the pattern of electric field lines in this arrangement.
View SolutionThe Gaussian surface for calculating the electric field due to a charge distribution is
View SolutionA charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).
View SolutionIt is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss's theorem because:
View SolutionA few spherical equipotential surfaces are shown in the figure. The electric field at any point, at a distance x from the centre, is
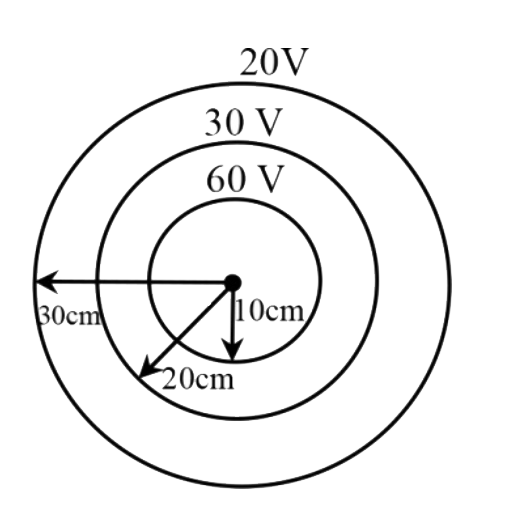
View Solution