Consider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
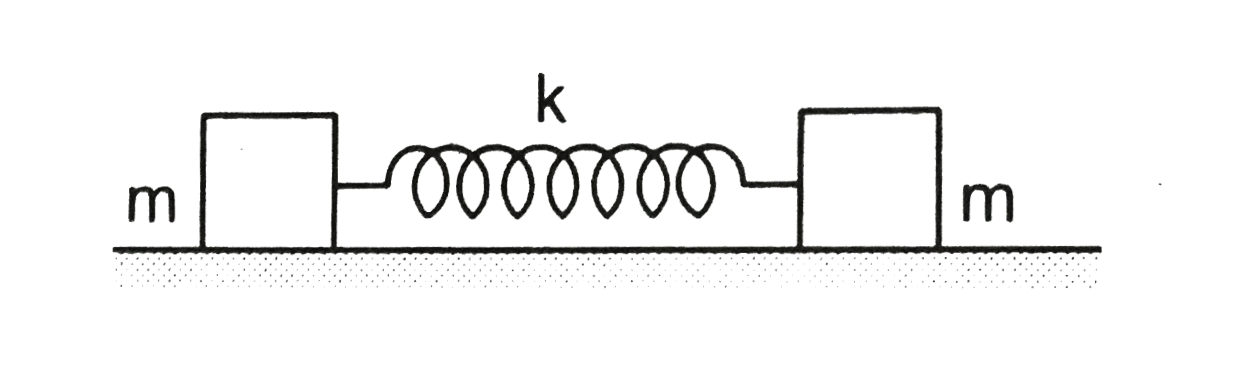
The correct Answer is:T=2π√m2k
The centre of mass of the system should not change during the motion.
So,if the block m on the left moves towards right a distance x the block on the right moves towards left a distance x so total compression of the spring is 2x.
By energy method
12k(2x)2+12mv2+12mv2=C
→mv2+2kx2=C
Taking derivative of both sides with respect to t.
m2vdvdt+2k×2xdxdt=0
∴ma+2kx=0
[because v=dxdtanda=dvdt]
→−ax=2kmω2
→ω=√2km
→Time period
T=2π√m2k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMAChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 2 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMAChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Exercises
Explore 32 Videos
Similar Questions
Consider a situation shown in the figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute S.H.M. calculate the time period.

View SolutionAsume that as narrow tunnel is dug between two diametricaly opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that ilf a particle is relesed in this tunel, ilt wil execute a simple harmonic motion. Calculate the time period of this motion.
View Solution
Knowledge Check
A pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
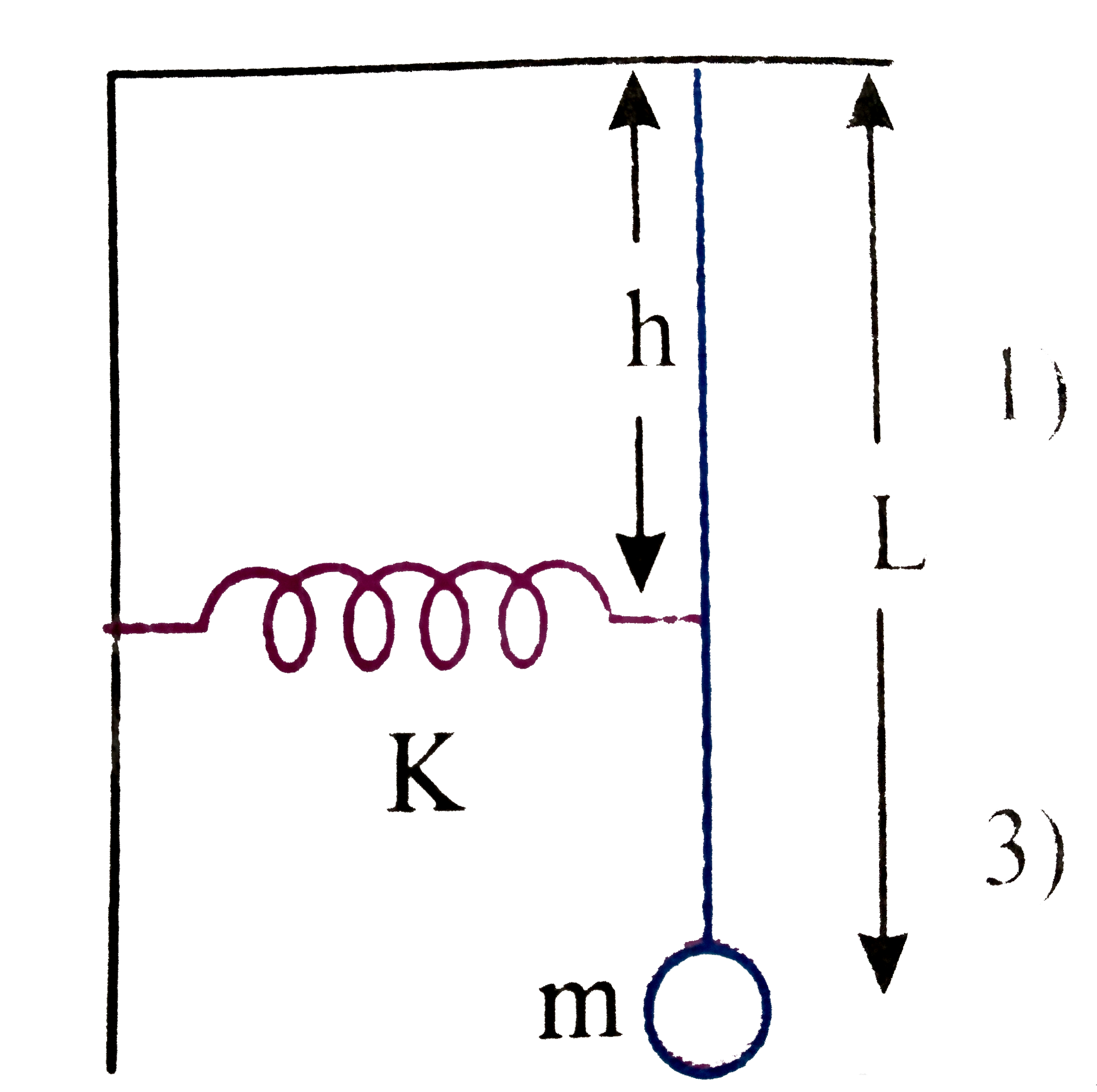 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2The distance moved by a particle in simple harmonic motion in one time period is
AAB2AC4ADzeroif a boby is released into a tunal dug across the diameter of earth, it executes simple harmonic motoin with time period
AT=2π√RegBT=2π√2RegCT=2π√Re2gDT=2 seconds
A magnetic dipole of magnetic moment M is suspended by a string in a uniform horizontal magnetic field as showo in figure. If in horizontal plane this dipole is slightly tilted and released, show that it will execute simple harmonic motion and find its oscillation period. Consider the dipole as a uniform rod of mass m and length I.
View SolutionWhat is the direction of displacement in a simple harmonic motion ?
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
View SolutionFind the period of the oscillations of the devices shown in figure if m is displaced slightly.
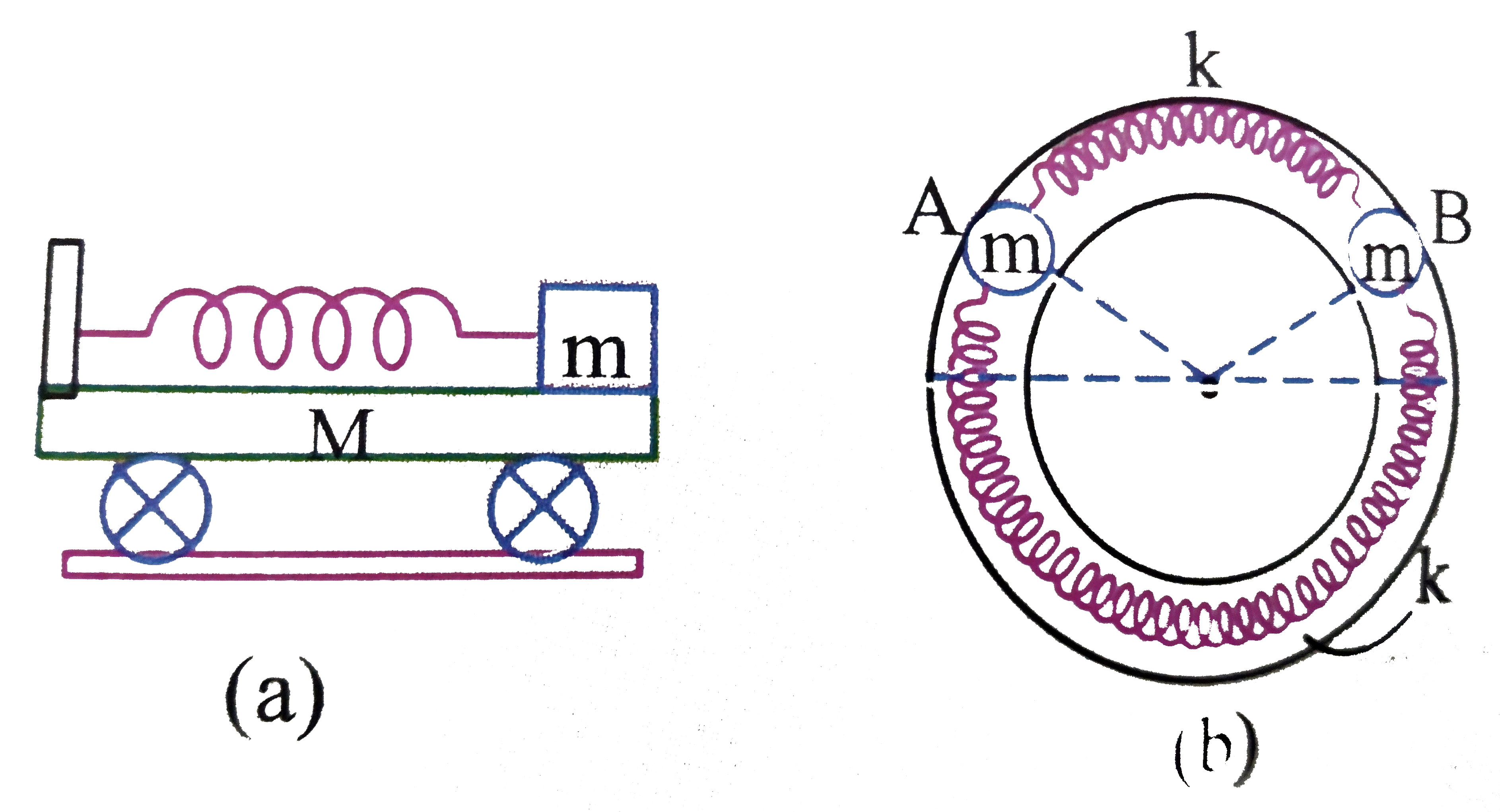
View SolutionA rectangular plate of sides a and b is suspended fropm a ceilling by two parallel strings of length L each figure. The separation between the strings is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute harmonic motion. Find the time period.

View Solution