Demostrate that molar heat capacity of a crystal at a temperature , where is the Debye temperature, is defined by Eq. (6.4f)
We use the formula (6.4d)
In the limit , the third term in the bracket is exponentially small together with its derivatives.
Then we can drop the last term
Thus
Now from the table in the book
.
Thus
Note: Call the term in the bracket above- . Then
The maximum value of is a finite+ve qauntity for . Thus
we see that is exponentially small as . So is .
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction
42 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Knowledge Check
The molar heat capacity for a gas at constant T and P is
A3/2 RB5/2 RCdepends on atomicity of gasDinfinity (∞)Two liquids of specific heat ratio 1:2 are at temperature 2θandθ
Aif equal amounts of them are mixed, then temperature of mixture is 1.5θBif equal amounts of them are mixed, then temperature of mixture is 43θCfor their equal amounts, the ratio of heat capacities is 1:1Dfor their equal amounts, the ratio of their heat capacities is 1:2.
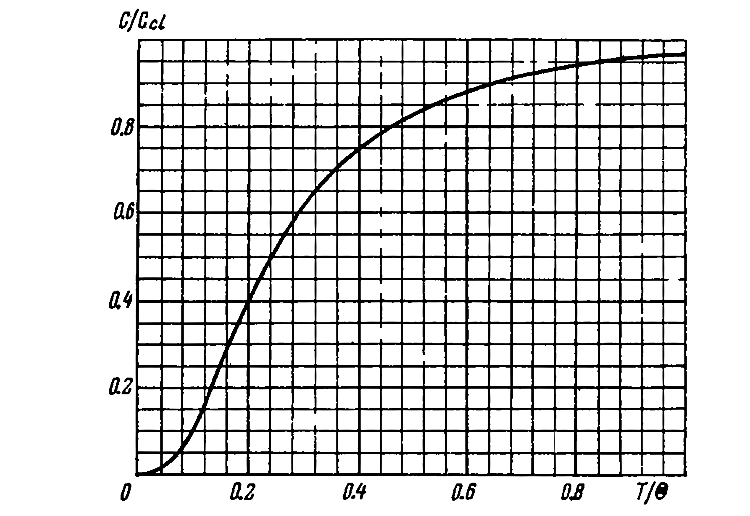
Figure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here Ccl is classical heat capacity Θ is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature T=65K its molar heat capacity is equal to 15J(mol.K),
(b) the molar heat capacity of aluminum at T=80K if at T=250K it is equal to 22.4J(mol.K)
(c )the maximum vibration frequency for copper whose heat capacity at T=125K differs form the classical value by 25%.
View SolutionDerive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature T if the Debye temperature of the chain is equal ot Θ. Simplyfie the octained expression for the case T>Θ
View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
View SolutionWhat is the most likely value for CT (molar heat capacity at constant temperature) ?
View SolutionThe motor heat capacity of rock salt at low temperatures varies with temperatures according to Debye's T3 law.
Thus, C = kT3θ3, where k = 1940 Jmol−1Ko−1, θ = 281 K)
Calculate how much heat is required to raise the temperatures of 2 moles of rock salt from 10 K to 50 K?
View SolutionIf a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View Solution
